碰撞出来的圆周率（中）

二、物理

先来看物理部分。

假设物体A质量为m，物体B质量为M，令k为M/m的（正）平方根，也即k²=M/m。为了一般性起见，我们不要求k是10的幂，甚至不要求k是整数，只要求k≥1，也即A的质量不大于B。在整个过程中，物体A的速度v(t)和物体B的速度V(t)都是时间t的函数，我们令向左的速度为正速度，这样向右的速度就被表示为负的。假设物体B初始的（向左的）速度为W。整个过程中动能守恒，于是在任意时刻t我们都有
    1/2MV(t)²+1/2mv(t)² = 1/2MW²
也即
    (V(t)/W)²+(v(t)/(kW))² = 1
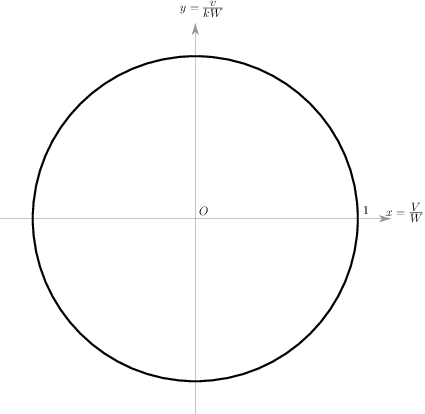
这意味着在任何时刻t，点(V(t), v(t))都处于一个固定的椭圆上。如果我们作一个拉伸变换，定义新的关于t的函数x(t)=V(t)/W，y(t)=v(t)/(kW)，上面的公式就变成了
    x(t)²+y(t)² = 1
也就是说不同时刻t所对应的p(t)=(x(t), y(t))都处在以原点为中心，以1为半径的圆上。

我们注意到，当在某段时间t₁到t₂之间没有发生过碰撞，那么这段时间里的v(t)和V(t)都是不变的，于是这段时间里点p(t)也是不变的。在整个过程中只会发生有限次碰撞，所以p(t)在坐标系中的图像将只有有限个点。下面我们将考察在某次碰撞前后，点p(t)会怎样变化。

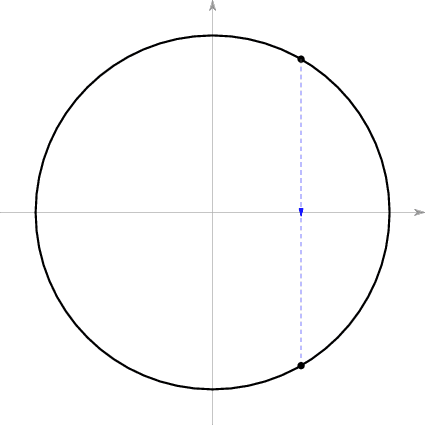
如果是物体A和墙的碰撞，那么在碰撞前A向左运动，碰撞后则向右运动，而速度大小相同；物体B则保持原来的运动状态。这意味着在碰撞前p(t)处于x轴上方，碰撞后则处于x轴下方，和原来的点以x轴对称。

如果是物体A和B的碰撞，那么在碰撞前A必定静止或是在向右运动，不存在A和B都向左运动且B的速度大于A而与A相撞的可能（证明略，只指出一点：如果A正在向左运动，表明前一次碰撞发生在A和B之间），这意味着在碰撞前p(t)处于x轴上或是在它的下方。碰撞前后动量守恒，即
    MV(t)+mv(t) = C
其中C在碰撞前后是个常数。如果将上式两边都除以MW/k，我们得到
    kV(t)/W+v(t)/(kW) = kC/(MW)
也即碰撞前后
    kx(t)+y(t) = kC/(MW)
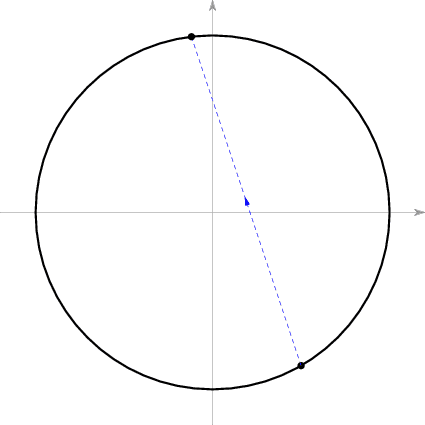
上式等式的右边还是一个常数。这意味着碰撞前后的p(t)在同一条斜率为-k的直线上。综合上述结论，碰撞前后的p(t)的图像变化应该如下图所示，其中虚线的斜率为-k。

于是我们就得到了整个过程中p(t)变换模式：从点(1, 0)开始（对应着B刚开始以速度W向左运动，还未撞上A时的状态），交替地以斜率为-k的直线和以平行于y轴的直线成之字形在圆周上截出的点。下图是k=3时的情形。每一条蓝色虚线段代表一次碰撞，箭头方向则代表了此次碰撞前后系统状态（即点p(t)）转换的方向。

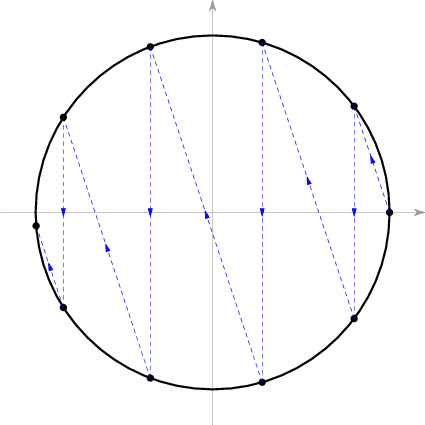
于是碰撞次数就是蓝色虚线段的数量，或者说是圆周上的p(t)图像的点数减1。这样，一个物理问题被转化为一个几何问题：从点(1, 0)开始，按照上述方法，交替地以斜率为-k的直线和以平行于y轴的直线成之字形在圆周上截出的点会有几个？而这个问题，即便从直觉上也可以感到它会和圆周率π很有关系。

顺便要指出的是，我们发现转换后的问题仅和k的值有关，或者说仅和物体B和物体A的质量比有关，而和物体A和物体B的具体质量、初始的推动速度W或是物体A和墙的距离等值无关。