碰撞出来的圆周率（下）

三、几何

在上节中我们把原来的物理问题转化成了一个几何问题：从点(1, 0)开始，交替地以斜率为-k的直线和以平行于y轴的直线成之字形在半径为1的圆周上截出的点会有几个？本节则将用几何的方法来解决此问题。

首先我们要解决的问题是，按照上述交替截圆周的方式，最后会以什么样的方式结束？也就是说，最后一个点的位置会是什么样的？答案是，这个点是最后一点当且仅当它落在下面这条红色的弧上，包括两个端点。其中红色虚线的斜率为1/k；蓝线为圆周在Q点的切线，所以它垂直于红色虚线，斜率为-k。因为圆半径为1，红弧的长度等于它所对应的圆心角大小，为arctg(1/k)。

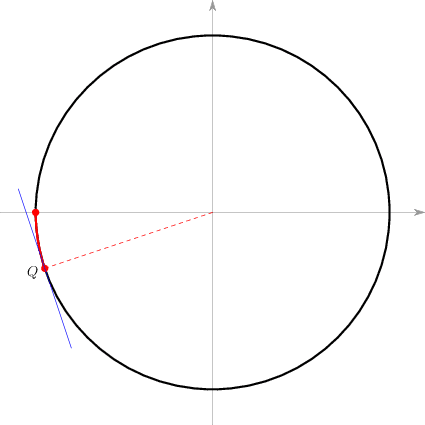
这一点可以从物理和几何两方面来论证。

从物理图景来解释的话，不再发生碰撞的充要条件是物体A和物体B均处于静止或向右运动的状态，而且A的速率小于等于B的速率，即V(t)≤0，v(t)≤0且V(t)≤v(t)。翻译成函数x(t)和y(t)的语言，就是x(t) ≤ ky(t) ≤ 0，对应到圆周上，就是上图里的红弧。

从几何上说，如果圆周上的一个点p处于x轴下方或等于点(1, 0)，而且它不在上面那条红弧上，那么通过它的斜率为-k的直线必定处于上图蓝色切线的右上方，会在圆周上截出一个处于p的左上方的点p’来。换句话说，p必定不会是之字形截点过程的终结点。更进一步，如果上面这个新点p’不在红弧上（此时它会是截点过程的终结点），那么它必处于x轴的上方。同样，如果圆周上的一个点p在x轴上方，那么通过它的和y轴平行的直线必定可以在圆周上截出一个在x轴下方的点来，p也不会是之字形截点过程的终结点。

通过归纳法，从(1,0)出发的之字形截点过程必然可以一直持续下去，直到到达上图红弧上的一点。而一旦到达红弧，就既不可能用斜率为-k的直线向左上方截点，也不可能用和y轴平行的直线向下截点：它必然是终结点。

我们看到物理和几何的方法都得到了同样的结论：之字形截点过程终结，当且仅当截点出现在上述的红弧上。

而截出终结点的方式有两种，下面我们分别讨论。

第一种方式是终结点被斜率为-k的直线所截出。在物理上对应的过程是倒数第二次物体A和墙相撞向右弹回，并追上正向右运动的物体B，进行了最后一次撞击；撞击后物体A和B仍朝右运动，只是A的速率小于等于B。第一节中质量比为100的动画中的撞击过程就是这样结束的。在k=3时终结点也是这样被截出，下面我们以此为例说明。

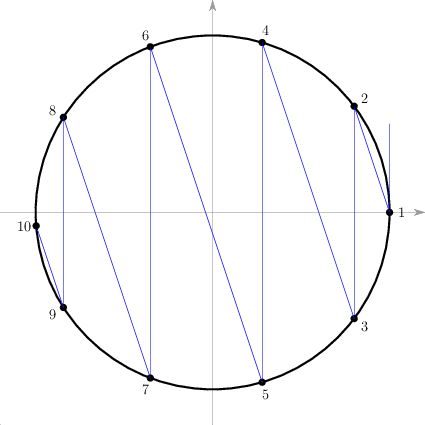
在图像中我们将每个点标了号，并通过初始点1作了切线。这样除了最后一点10外，每一点都对应着以它为顶点，由两条蓝色射线形成的角。因为所有斜率为-k的直线都平行，所有平行于y轴的直线都平行，于是角1到角9依次两两都是平行直线的内错角，它们均相等，其正切是1/k，故等于arctg(1/k)。它们是圆周角（角1是弦切角，可以看作是圆周角的特殊情况）。从中学平面几何里我们知道，它们对应的圆弧长度均相等；因为圆半径为1，它们所对应的弧长是两倍的圆周角大小，即2arctg(1/k)。在k=3时，弧1-2、弧1-3、弧2-4、弧3-5、弧4-6、弧5-7、弧6-8、弧7-9，弧8-10的长度均是2arctg(1/3)；而弧9-10的长度小于此值。出现最后这段弧长会等于前面的弧长的情况仅当终结点正好是点(-1, 0)，这是k=1也就是物体A和物体B质量相等的情况。

第二种方式是终结点被平行于y轴的直线所截出。在物理上对应的过程是倒数第二次物体A与物体B相撞后向左运动，最后撞在墙上向右弹回，但此时它的速率已小于B的速率，再也追不上B。这是第一节中质量比为10000的动画中的撞击过程结束的方式，同样也是k=4时的情况。下面我们以k=4为例说明。

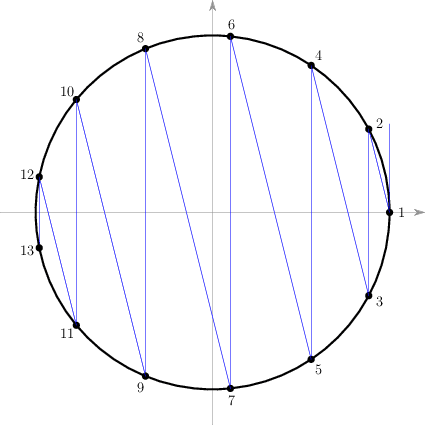
和k=3的情况很相似，圆上的截点把圆周截成了若干段长度为2arctg(1/k)的弧，以及最后一段弧12-13。最后这段弧的长度总是小于等于两倍的红弧（因为最后一点须在红弧内），也就是2arctg(1/k)。

综合上述两种方式，我们就得到结论：之字形在半径为1的圆周上截出的点的个数，正是圆周的长度除以2arctg(1/k)的结果的整数部分再加1，这个1对应着那段比较短的弧。（严格地说，如果圆周的长度除以2arctg(1/k)的结果恰好是整数，如当k=1时，那么就不用加这个1了，这一点将在后面补充说明）。或者说，碰撞的次数（它等于点的个数减1）就是圆周的长度除以2arctg(1/k)的结果的整数部分。但半径为1的圆周的长度正是2π。这一下，碰撞次数和圆周率的关系可谓昭然若揭，剩下的只不过是一点计算细节罢了。

碰撞的次数为圆周长2π除以2arctan(1/k)的整数部分，也就是[π/arctan(1/k)]，其中[]代表取整运算。当k大于等于1时，arctan(1/k)总比1/k大一点，但差不了多少；更精确地，π/arctan(1/k)和π/(1/k)=kπ差不多大小，k越大，这个差就越小。这一点可对f(x)=π/arctan(x)-π/x在零点附近作泰勒展开并作估计即可，这要用到数学分析知识，这里就不具体进行了。于是[π/arctan(1/k)]和[π/(1/k)]=[kπ]一般来说是相等的。

总的来说，在理论上[π/arctan(1/k)]和[kπ]有极小的可能差1。一种可能是上述的圆周的长度除以2arctg(1/k)的结果恰好是整数的情况，那么很好，因为arctan(1/k)总比1/k大一点，于是[kπ]等于[π/arctan(1/k)]-1，正是圆周上的点个数减1。

另一种可能则相当麻烦。如果π/arctan(1/k)和kπ恰好在某个整数的两侧，就如2.00001和1.99999在2的两侧那样，相差极少，取整结果却差1。为了对这个细节做精确估计，Galperin差不多用了论文的三分之一篇幅来作相当繁琐的讨论，也没有完全排除这种可能性。但对于我们来说，即便[π/arctan(1/k)]和[kπ]真的差1也不是太有所谓，因为这无非是在说，碰撞的次数和π的前几位数几乎一样，最多差1。这并不影响结果的漂亮，也不影响我们对为何初始的碰撞问题会和圆周率有出人意料却在数理之中的联系的理解。所以我们接下来就当这种可能性不存在。

这样我们就知道，总的碰撞次数是[kπ]。于是最终结论就显而易见了，在k=10时碰撞次数是[10π]，k=100时碰撞次数是[100π]，等等等等，就是圆周率π的前几个数字。可以看出，如果不用十进制而是用其他进制，也会有类似的结果。比如说在二进制下，圆周率π约等于11.0010010000111111……，如果我们取k=2⁵=32，也就是质量比为2¹⁰=1024时，模拟结果表明会发生100次碰撞：

而100在二进制下的表示为1100100，恰是π的二进制表示的前7个数字。

---

参考文献：

[1] Gary Antonick, The Pi Machine, Numberplay, Wordplay Blog, http://wordplay.blogs.nytimes.com/2014/03/10/pi/

[2] Gregory Galperin, Playing pool with π (the number π from a billiard point of view), Regular and Chaotic Dynamics, Volume 8, Number 4, Pages 375–394 (2003).