Voderberg铺嵌图的绘制（下）

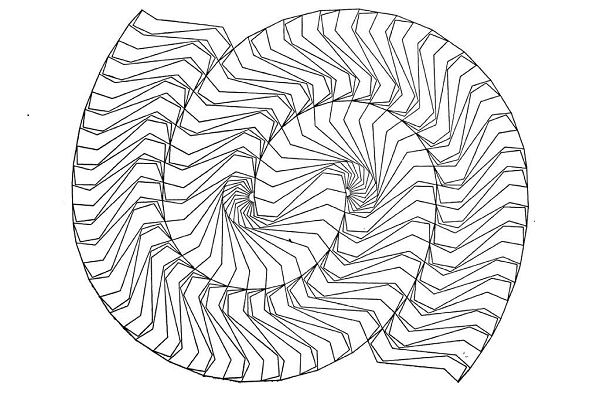
在这个下篇中我们主要讨论Voderberg拼块。由于它的特殊性，无法生成大顶角的拼块，所以我们在示意图中取顶角18°，而非上篇中的30°。

四、Voderberg拼块的奇特性

在本文上篇中我们讲到，事情有点蹊跷。Voderberg拼块看起来既不是S型的也不是C型的，因为它虽然满足两侧边全等条件，但它的侧边既非中心对称，又非轴对称：

下图是马丁·加德纳介绍Voderberg拼块和Goldberg三角替换法的文章中的附图（注意左下角Voderberg拼块和三角形的相对位置），许多网站上也有类似的图，似乎也暗示了上图中的替换规则。

使用这个替换规则，在只有两个三角形侧边相拼时到也可以拼合：

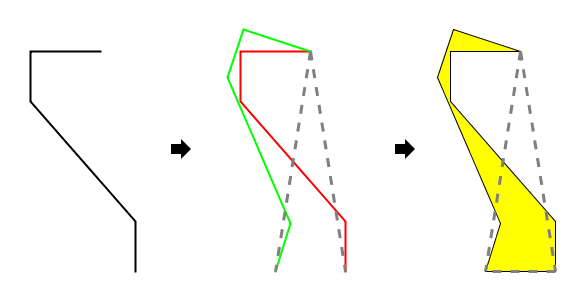
如果仔细观察上图右边顶角交错的情况可以看出，两块拼块拼合的交界处所对应的原三角形的侧边，其实是外侧的那两边，而不是原三角形拼合的那两边。看起来似乎在左边的那个Voderberg拼块，其实替换的是右边那个顶角向上的三角形，右边的拼块替换的则是左边顶角向下的三角形；如果说原来的三角形是背对背拼合的，用了这个替换规则后，两块Voderberg拼块成面对面的了！

更重要的是，在这个拼合中，替换后的拼块范围已经溢出了原来两个等腰三角形的两条底边，和这两个三角形以底边相拼的三角形按规则替换成Voderberg拼块后会与已有拼块相重叠：

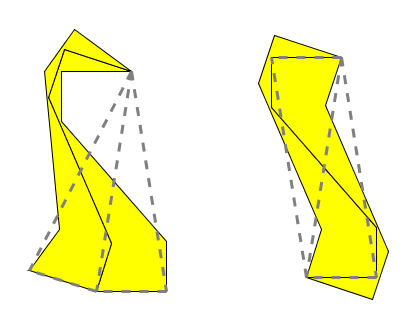
但Voderberg拼块真的有这么例外吗？如果我们进一步观察，就会发现，前面那个面对面拼合的交接处其实就是一条中心对称曲线。这就提示我们，我们可以把Voderberg拼块看作是这条中心对称曲线生成的S型拼块：

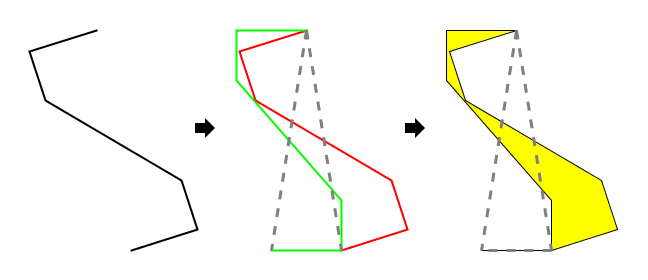
在这种观点下，Voderberg拼块本身完全仅由侧边包围，而真正“底边”却在它的外部（红色和绿色曲线末端的连线）。这个底边和侧边一起围出的面积为零，所以可以忽略。注意到此时Voderberg拼块的形状和前面相比并未改变（除去那个可忽略的小尾巴），但它的三角替换规则变了。在这样的替换规则下，两个拼块拼合的情况也正常了，原本三角形背对背的拼合仍保持为拼块背对背的情况；底边也不会出现溢出的现象：

于是我们可以得到Voderberg拼块的Goldberg铺嵌：

注意到螺旋末端的那几个小尾巴，就是那条不围住什么面积的“真正的底边”，在绘制用于展示的图时当然得去掉。

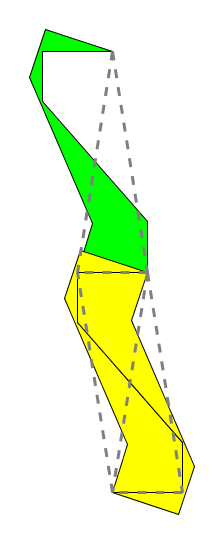
所以我们知道Voderberg拼块并非一种例外，它其实是一种S型拼块，只是真正的底边在拼块外部，一般不画出来。这同时也提醒我们，上面这样的Voderberg拼块只是一个特例而已——在那条生成Voderberg拼块的中心对称曲线上，只有上下两段长度为原三角形底边的线段的形状、长度及位置是不能变的（否则无法造成“真正的底边在拼块外部”的效果），当中的这部分，则可选得比较自由，只要仍保持中心对称，以及能够生成拼块这两个条件：

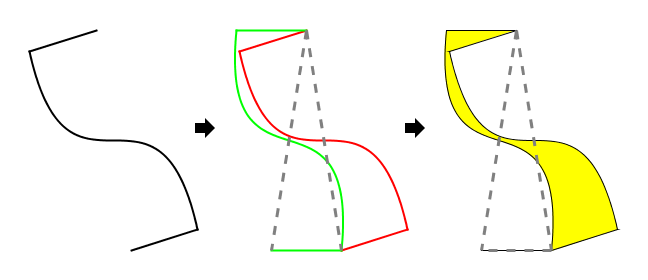
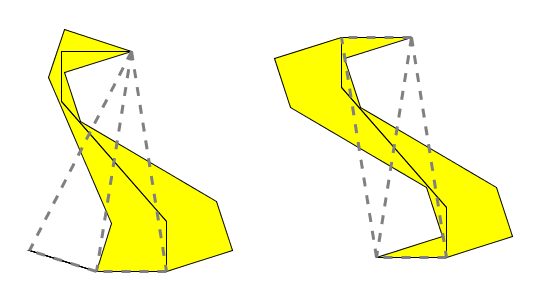
这种拼块也同样满足“两个几乎围绕一个”和“两个几乎围绕两个”的性质：

在Waldman的[4]中首先提出了Voderberg拼块侧边生成曲线中中间这段选取的自由性，但是因为他不以本文中中心对称曲线的S型拼块的观点来分析Voderberg拼块，所以在生成拼块时必须固定三段线段，而非本文中的两段。

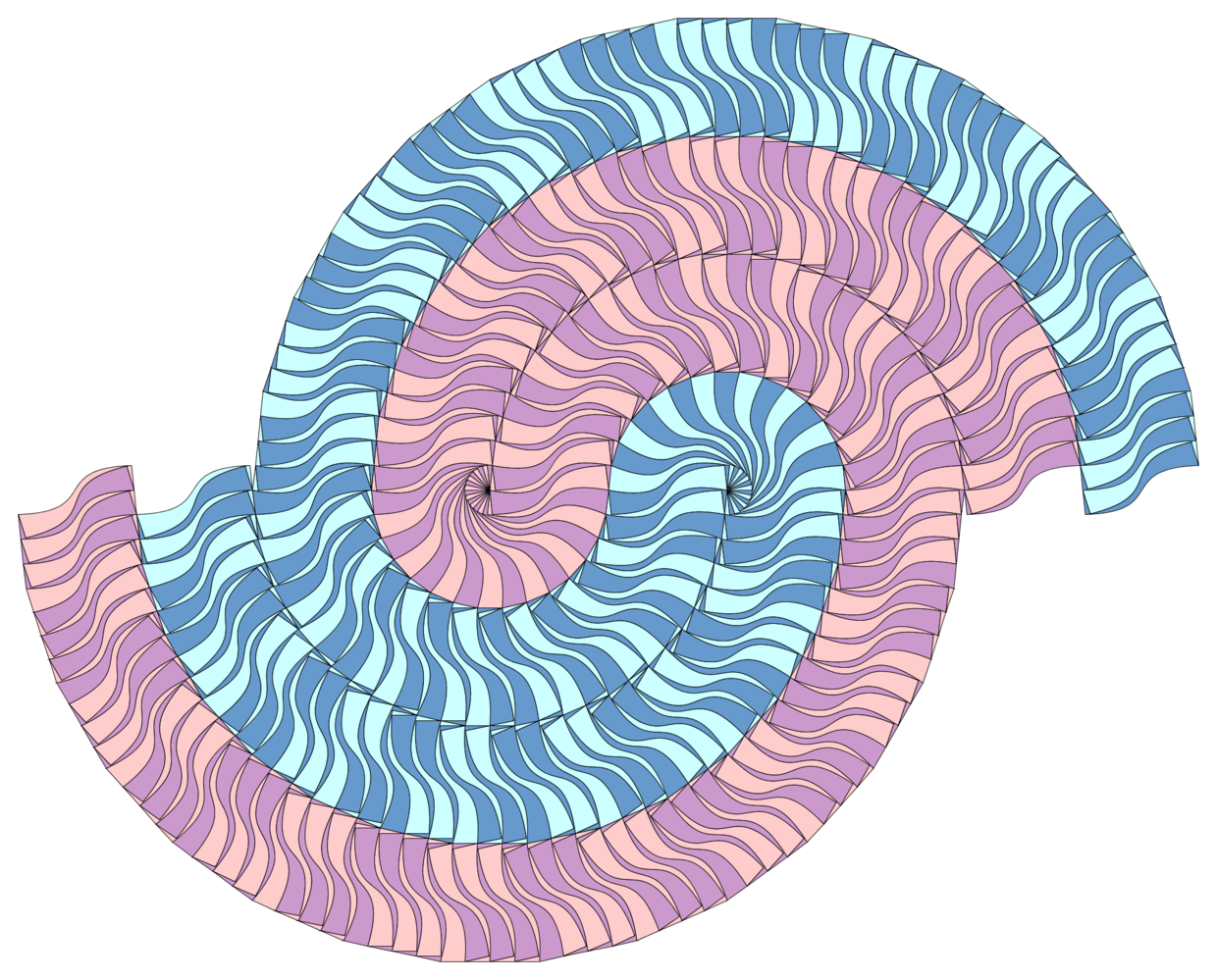
最后当然要来一张这样的Voderberg拼块的铺嵌作为展示用的大图，顶角12°，交错数为2：

五、C型Voderberg拼块和更一般的Voderberg拼块

上面这种推广了的S型Voderberg拼块自然地会让人想到，是否有类似的“真正的底边在拼块外部”的C型拼块？它的特点应该是由一条轴对称曲线生成，最末端是一条线段，旋转后这条线段看起来恰好成为拼块的底边，而真正的底边在拼块外部。

它是下面这样的轴对称曲线：两端是两段线段，它们之间的夹角是Goldberg三角铺嵌中三角形的顶角；而这两条线段之间的连线则可以比较自由地选取，只要满足整条曲线轴对称，以及能够生成拼块这两个条件：

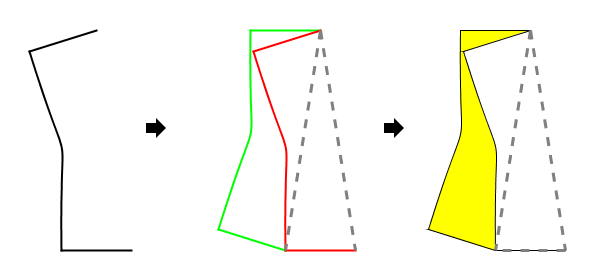
很遗憾，它没有象S型Voderberg拼块那样的“两个几乎围绕一个”和“两个几乎围绕两个”的奇特性质。因为当两个拼块顶角交错相拼时，其中一个必须是另一个的镜像，于是两个拼块上的长嘴会朝着同一个方向，无法象S型拼块那样利用这两个长嘴包住一个区域。只是因为“真正的底部在外”的特点和上篇第三节中讲到的C型拼块替换三角时需考虑镜像拼块的要求，它的Goldberg铺嵌细看起来复杂一些。

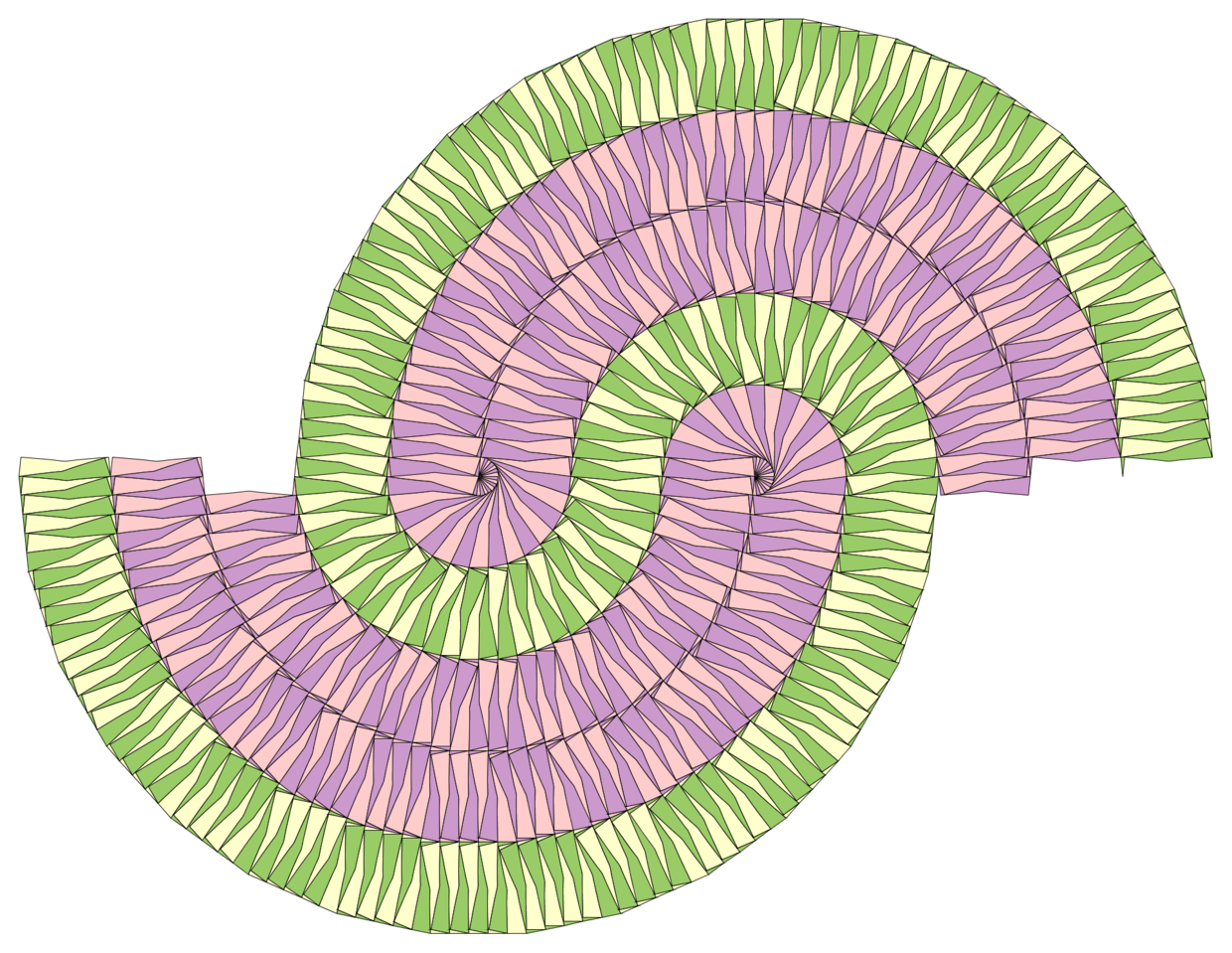
仍旧回到S型拼块的情形。我们还可以由着“真正的底边在拼块外部”这条思路再进一步：还有没有更加一般化的“真正的底边在拼块外部”的情况？它其实就是Casey Mann在[3]中介绍过的，也同样是由Goldberg提出的“一般化Voderberg拼块”。

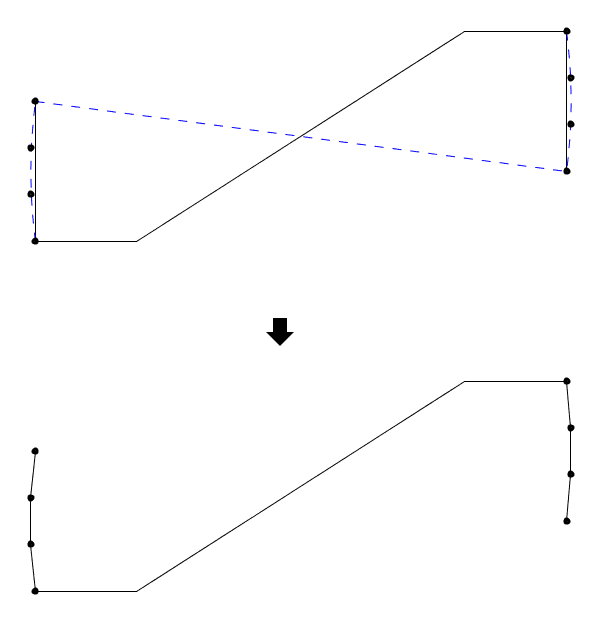
它的侧边生成曲线按如下方法构造。首先取前面那条中心对称的普通Voderberg拼块的侧边生成曲线，按下图分别以曲线两端为圆心，以两端距离为半径作圆弧，圆弧的两端恰好是那条特殊线段的两端。对于任意大于或等于2的自然数n，在每条圆弧上取n+1个点（包括那两个端点），将圆弧分为n等分。将这些点顺次连在一起得到的两条折线，用这两条折线取代原来的那两条线段，保持其他部分不变，我们就得到了一条新的中心对称曲线。例图中我们取n=3：

如果原来那个普通Voderberg拼块的顶角是α，那么上面这条新的曲线就可以用来生成一个顶角为α/n的一般化Voderberg拼块。例图中α=18°，于是新拼块顶角为6°：

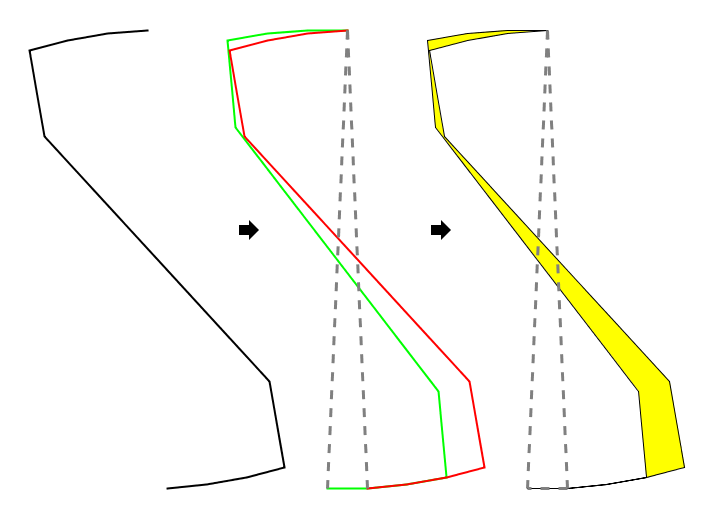
和普通Voderberg拼块的情形类似，这里有个面积为零的尾巴，只是比较长，同样可以忽略。如果说普通Voderberg拼块的真正底边还和拼块沾上那么一点，一般化Voderberg拼块的真正底边完全和拼块脱离了。

一般化Voderberg拼块有“两个几乎围绕2n-1个”和“两个几乎围绕2n个”的性质。在n=3时的示意图：

当然，因为一般化Voderberg拼块是S型拼块，它同样有Goldberg铺嵌。

当然读者还可以考虑C型的一般化Voderberg拼块，中间那段曲线取得比较自由的情况，甚至还可以考虑拼块底边不是直线的情况，等等等等。不过对这些情况本文恕不赘述。

---

参考文献：

[1] 安安以迁迁, 《Voderberg拼块的妙用：围绕数为2的拼块》, 科学公园.

[2] Martin Gardner, Penrose Tiles, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems., W. W. Norton & Company, ISBN: 978-0393020236.

[3] Casey Mann, A Tile with Surround Number 2, The American Mathematical Monthly 109(4): 383-388 (2002)

[4] Cye H. Waldman, Voderberg Reimagined, http://curvebank.calstatela.edu/waldman10/voderbergcornu.pdf (2014)