数学科普
Voderberg铺嵌图的绘制(上)
作者:安迁
《Voderberg拼块的妙用:围绕数为2的拼块》(下面称为“《V》文”)中展示了几张Voderberg铺嵌图样,有圆盘状放射形和螺旋形的。本文将比较详细地描述此类铺嵌的绘制方法。不过,这里说的“绘制方法”是指其中的数学原理;而要将它真正实现,需要读者使用绘图工具自己动手。
本文中一些图片可点击放大,以便读者看到细节。
一、Goldberg铺嵌
本文使用的方法是Michael Goldberg在1955年提出的三角替换法,这种方法因被马丁·加德纳在科普文章中介绍而广为人知。在铺嵌理论中,替换法是用来生成某些铺嵌的常规方法。如著名的彭罗斯P3铺嵌(通常说的彭罗斯铺嵌共有三种,分别为P1,P2和P3),构成这个铺嵌的两个拼块是如下图左边所示的两个边长相同的菱形,它们的锐角分别为36°(称为“瘦菱”)和72°(称为“胖菱”),拼块间的拼嵌规则是红绿线必须连续。执行替换法时,它们的替换规则如下:
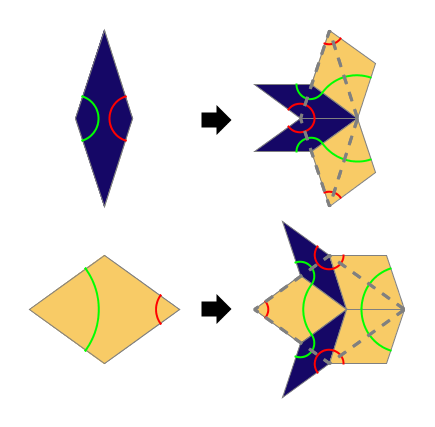
图中虚线部分分别是原有的胖菱和瘦菱的位置。替换操作就是将左边原有的瘦菱或胖菱换成右边所示的较小版本瘦胖菱的组合。这样的替换可以反复迭代进行,将小版本菱形按规则替换成更小版本的菱形。
下图展示在这个规则下,一个大的胖菱在若干次迭代替换后出现彭罗斯铺嵌图样的过程(每次操作后去掉完全不在原大胖菱范围内的那些拼块,以使图形外围简洁):
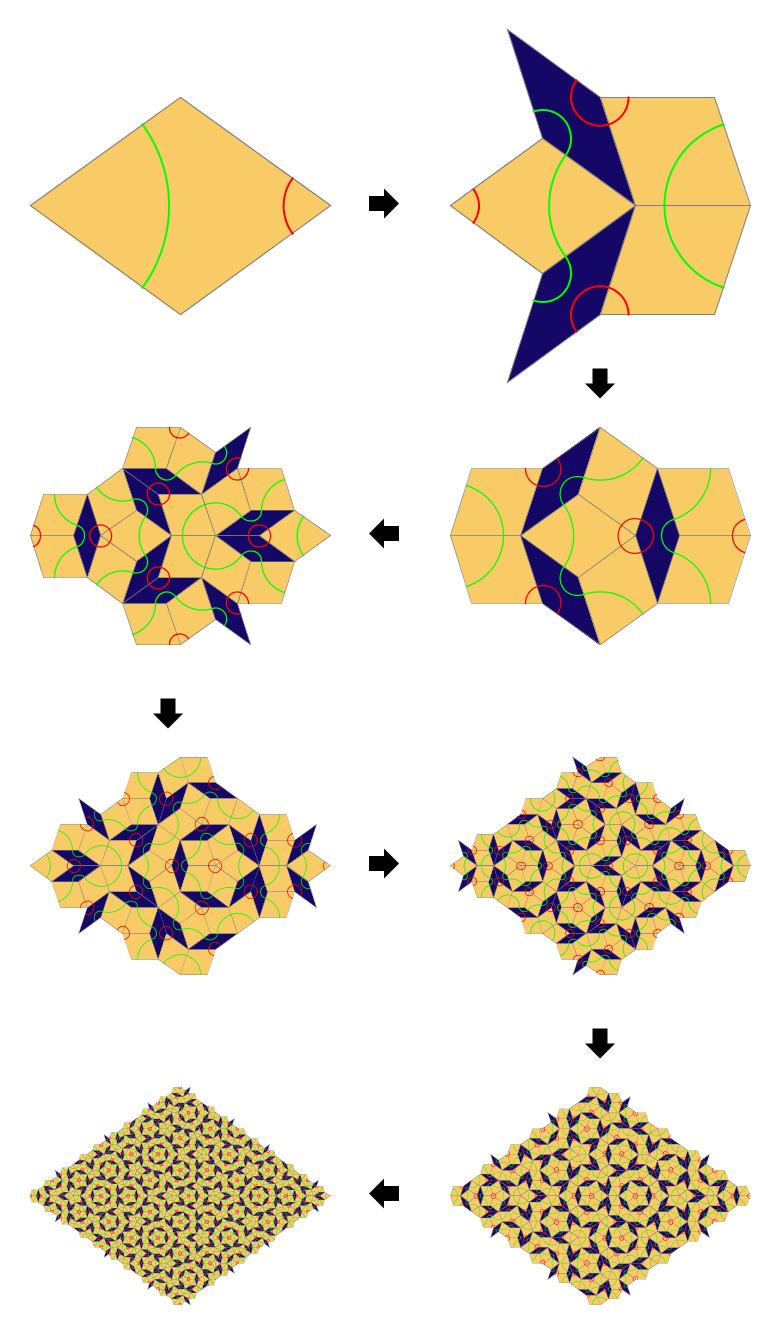
彭罗斯铺嵌是一个极为有趣的话题,它是所谓的“反周期铺嵌”的一个重要例子。要对它进行一个一般性的介绍,篇幅恐怕也会超出本文现有的整个长度。所以这个话题在本文就到此为止,有兴趣的读者可在网上搜索相关资料。在这里,读者只需要了解到铺嵌理论中的替换法是常用而强大的工具,它大约是怎样一种方法就可以了。本文介绍的三角替代法从替代规则上来说要远比上面的彭罗斯铺嵌中的替换法简单,它只是将一个等腰三角形替换为一个顶角和底边位置相同但两条侧边扭曲了的图形,而且没有迭代替换过程。
首先要介绍的是最基本的Goldberg等腰三角形铺嵌平面的方法,如何把其中的等腰三角形替换为其他图形的方法则将在后面叙述。
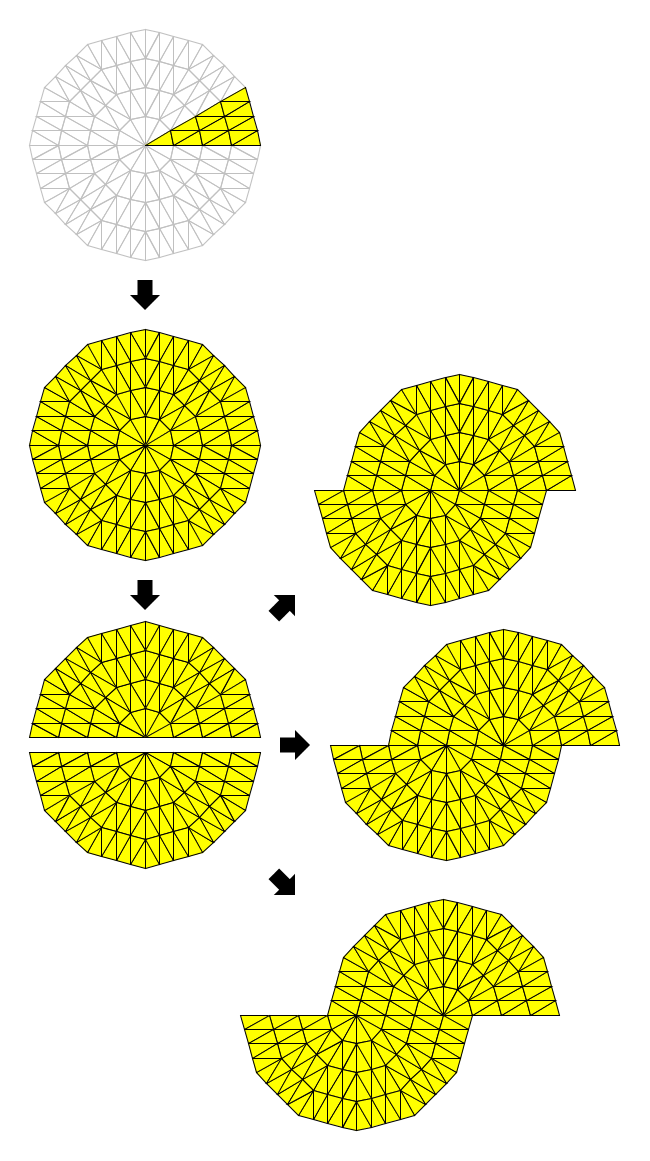
如上图所示,开始的基本图形是等腰三角形拼块拼成的大等腰三角形。它的规模也就是小三角形堆砌的层数从理论上来说可以任意选取,如果选无限层,后面就会得到一个对整个平面的铺嵌;而实际绘制中则按照需要和电脑的能力来选择。以这个大三角形为原型绕顶角旋转铺嵌,则可以得到一个放射形的圆盘铺嵌(其实是个正多边形),而这个圆盘可以切成上下两半,错开一个或几个小三角形侧边的长度的位置再拼合,就可以得到螺旋铺嵌。错开的小三角形侧边的长度的个数我们称之为交错数。这个交错拼合的技巧,就是我在《V》文中说我们看到的螺旋只是一个心理效应的原因,因为螺旋仅因这个交错产生。Voderberg对他的螺旋形铺嵌的描述相当复杂,但正如马丁·加德纳指出的那样,Goldberg的方法让这种铺嵌的构造显而易见。
容易看出,构成铺嵌的基本单元的等腰三角形拼块,整个周角360°必须是它顶角角度的整数倍;如果考虑到要能将铺嵌切成上下两半,则必须是偶数倍。本文中我们在说明铺嵌原理时使用的图形一般将选择12倍,也就是顶角为30°的情况,因较宽的拼块容易显示和说明问题;而在显示铺嵌效果时则选择30倍,也就是顶角为12°的情况,因较细长的拼块造成的密集铺嵌在视觉上有比较良好的效果。
二、拼块需满足的条件
现在我们来看一下用什么样的拼块可以替换上面Goldberg铺嵌中的等腰三角形,而仍旧能得到合格的铺嵌;也就是说,替换后的拼块间既不重叠,也不留空隙。
如下图所示,在Goldberg三角铺嵌中,两个等腰三角形侧边间的拼合方式有两种:顶角聚在一起(左)或两个三角形一正一反,每个三角形的顶角都分别与对方某底角拼合(右):

先看前一种情况。如果把顶角聚在一起拼合的两个等腰三角形换成其他顶角和底边位置相同而侧边扭曲的图形,且仍要满足能互相拼合的条件,那么下图中红色的这条边既是左边拼块的右侧边,又是右边拼块的左侧边。所以这个拼块的两条侧边必须是相同的,只是以顶角为中心转动了一个角度(等于顶角的角度),我们称这条要求为两侧边全等:
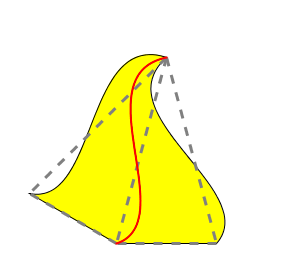
下面我们假定涉及到的拼块都满足两侧边全等的条件。
而按一正一反的拼法,从直觉上来说,可知这条侧边从中间向两边会具有某种对称性。事实上,存在下面两种情况,一种是以原三角形侧边中点为中心的中心对称(左),另一种是以原三角形侧边的垂直平分线为轴的轴对称(右):
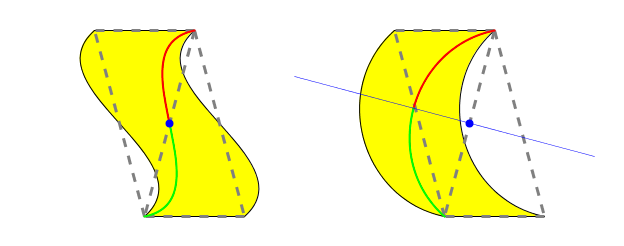
我们把这两种拼块分别叫作S型和C型的。取这两个字母的原因完全是因为字母形状的缘故。等腰三角形拼块既可以看作是S型的又可以看作是C型的。
我们注意到,在上图右边C型拼块的情况下,两块拼块无法只通过平移和旋转重合,它们其实是互为镜像的。这会给我们的铺嵌带来一定的麻烦,具体见后。
三、拼块的替换
而第二节的这个论证也可以反过来。
先举S型拼块的例子。随便取一条有两个端点的中心对称曲线,将它围绕一个端点转动一个角度(第一节末尾选定的那个),得到另一条曲线,然后把另外两个端点用线段连起来。如果这样三段曲线围成的形状是一个拼块,那么我们就得到了一个S型拼块,以及它对Goldberg三角铺嵌的替换规则:
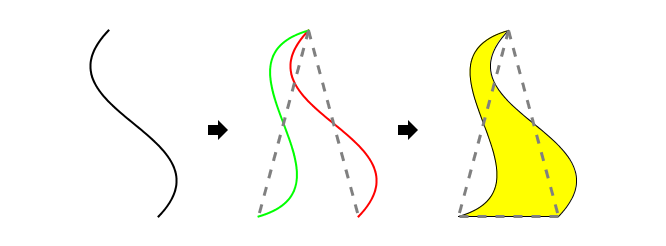
“这样三段曲线围成的形状是一个拼块”这个条件当然必不可少,而这个条件并不总是被满足的。如果转动后的曲线和原曲线或底边在非端点处相交,或原曲线本身就与底边在非端点处相交,我们就无法得到一个拼块。这个条件是否被满足取决于曲线的形状本身,也同样取决于转动的顶角角度,无法对一般情形给出一个简单的充要条件来判别。本文并不旨在从理论上严格论证Goldberg替换法适用的条件;在实际绘图过程中,具体试验观察三段曲线是否相交,大概才是最实用的手段。事实上,在本文下篇中谈到Voderberg拼块时,我们会遇见一种这三段曲线的位置比较奇特的情况。在本文接下去的部分里,我们都假设这个“形状是拼块”的条件成立。
回到我们上面图中这个拼块上来。使用这个拼块和替换规则,我们就得到了关于这个拼块的Goldberg铺嵌:

下面是用同一条曲线以顶角12°生成的拼块的Goldberg铺嵌,交错数为1:

C型拼块也类似。随便取一条有两个端点的轴对称曲线,如果也能按上面的方法得到一个拼块的话,那就有了个C型拼块,和它对Goldberg三角铺嵌的替换规则。
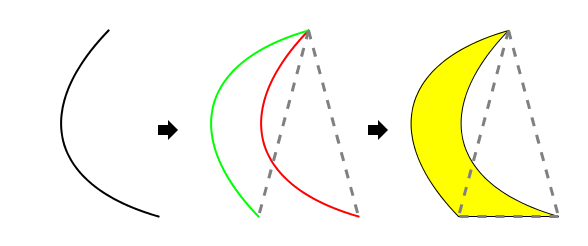
但在第二节里说到过,两个C型拼块侧边拼合时如果顶角错开,其中一个应该是镜像拼块。麻烦事就是:对Goldberg三角铺嵌进行替换时哪些地方要用到镜像拼块?等腰三角形的镜像就是它自己,所以进行Goldberg三角铺嵌时可以无视这个问题,可是对其他C型拼块就不能这么办了。
如下图所示,在Goldberg三角铺嵌图中有一些等腰三角形的顶角方向指向圆盘中心,我们称之为向心三角;而另一些则相反,我们称为离心三角。
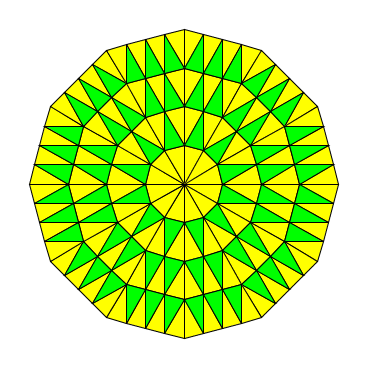
可以看到在上图中交错数为0的情况下,这两类三角在侧边拼合时,总满足“同类相拼顶角相聚,异类相拼顶角错开”的规律。所以此时上面问题的答案很简单:进行替换时,向心三角替换为原拼块,离心三角替换为镜像拼块(或反之):

可是如果对交错数大于0的情况也这样做,就会碰到困难,上下两块有无法拼合的地方:
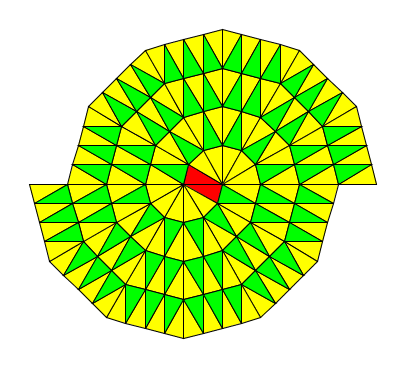
红色的两个三角形都是向心三角,却以顶角错开的方式拼在一起。这时必须把其中一个换成镜像拼块,但这意味着它旁边原本是镜像拼块的离心三角必须换成正常拼块,所以它所在的那半圈都必须这样反过来,但这又会影响到另外半块上的半圈……但是幸运的是,总能最后搞定:
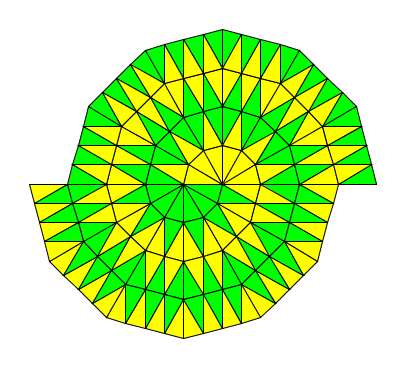
交错数为2,3,……的情况也类似。找到具体计算哪块应该是正常拼块,哪块是镜像拼块的数学公式的任务,就留给读者了——如果你能自己动手画图做到这一步,这事对你来说必定不难。
这样我们就得到C型拼块的各种Goldberg铺嵌:

当然也要展示一张顶角12°的大图:

那么对Voderberg铺嵌也可以拿上面的方法,用Voderberg拼块来替换一下Goldberg三角铺嵌中的等腰三角形就行了……且慢,下面这个Voderberg拼块(顶角18°),它到底是S型的还是C型的呢?

它的两条侧边看上去的确满足两侧边全等的条件,可是却既不是中心对称的也不是轴对称的。
Voderberg拼块真的很特殊吗?我们前面讨论的那些内容还能不能用在它身上,来绘制出Voderberg铺嵌图呢?请看本文下篇分解。
参考文献:
[1]安安以迁迁, 《Voderberg拼块的妙用:围绕数为2的拼块》, 科学公园.
[2]Martin Gardner, Penrose Tiles, The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems., W. W. Norton & Company, ISBN: 978-0393020236.