自绘Mandelbrot集合（五）

作者：安迁

十一、RGB颜色模型和真彩色

在继续修改程序以前，我们先要讨论一下和颜色相关的计算机语言知识。

在程序的第(9)部分给像素绘色时，其中表示颜色的参数rgb是一个32比特的整数。这个颜色代码使用的是通常所说的RGB颜色模型或红绿蓝颜色模型，并分别用8比特的数据来表示某颜色中的红、绿、蓝分量，即总共用24比特的数据来表示一种颜色，故可表示的不同颜色总共有2²⁴约为1677万种，即通常所说的“真彩色”方式。因为每种颜色分量都用8比特数据来表示，所以都有从0到255这256种可能性。数字越小，相应分量越小，反之亦然。

在上述方式下，一个32比特整数如何表示一种色彩？最高位的8比特通常被忽略（也有用作Alpha通道的，即表示此像素的透明程度，但在这里和我们无关）。接下去的8比特用来表示此颜色中的红色分量，然后是8比特的绿色分量，最后是8比特的蓝色分量。因为8比特数据恰好可以用两个十六进制数来表示，所以每种颜色也可用6位十六进制数来表示。

所以当我们拿到一个32比特整数rgb，想知道它代表了红绿蓝颜色分量分别为多少的颜色，只需将其表示为32位二进制形式，忽略其最高8位，然后依次每8位表示的就是此颜色的红绿蓝色分量（或者将其表示为8位十六进制形式，忽略其最高2位，然后依次每2位表示的就是此颜色的红绿蓝色分量）。比如十六进制数ABCDEF表示的颜色中，红色分量为AB（十进制数171），绿色分量为CD（十进制数205），蓝色分量为EF（十进制数239）。如果用Java程序写出来：

    int rgb = 0xABCDEF;
    int r = (rgb >> 16) & 0xFF; // = 0xAB
    int g = (rgb >> 8) & 0xFF;  // = 0xCD
    int b = rgb & 0xFF;         // = 0xEF

里面计算所得的r，g，b就是整数rgb所代表的颜色的红、绿、蓝分量。（&为按位与运算，“& 0xFF”即十六进制数只取最低两位。）

反之，如果我们知道了某颜色的红绿蓝分量（数字都在0和255之间），如何得到其颜色的整数表示？反过来即可，把分量写成二进制（或十六进制）形式，分段拼好：

    int r = 0xAB;
    int g = 0xCD;
    int b = 0xEF;
    int rgb =  (r << 16) | (g << 8) | b; // = 0xABCDEF

（|为按位或运算。）

十二、颜色渐变

颜色渐变也叫色彩梯度。给定两种颜色，可以非常不同（比如红色和绿色），如何实现从第一种颜色到第二种颜色的渐变，也就是在它们间插入一系列颜色，使得每两种相邻的颜色间的区别都不大？最简单的方式大概就是分别对两种颜色的红绿蓝分量进行线性插值，然后将得到的分量合成就得到了颜色（函数）。

比如说我们取一种颜色为红色（十六进制数FF0000，红色分量全满，其它两分量为0），另一种为绿色（十六进制数00FF00）。那么下面的函数，当变量f取0到1之间的实数时，我们就得到了从红色渐变为绿色过程的一系列颜色：

    int interpolation(double f) {
        int red = 0xFF0000;
        int green = 0x00FF00;

        // 将颜色拆成红绿蓝分量
        int r0 = (red >> 16) & 0xFF;
        int g0 = (red >> 8) & 0xFF;
        int b0 = red & 0xFF;
        int r1 = (green >> 16) & 0xFF;
        int g1 = (green >> 8) & 0xFF;
        int b1 = green & 0xFF;

        // 线性插值
        int r = (int) ((1 - f) * r0 + f * r1 + 0.5);
        int g = (int) ((1 - f) * g0 + f * g1 + 0.5);
        int b = (int) ((1 - f) * b0 + f * b1 + 0.5);

        // 将红绿蓝分量拼合
        return (r << 16) | (g << 8) | b;
    }

代码很容易懂：先是把红色red和绿色green拆成各分量，然后再以变量f为各分量作线性插值并四舍五入取整，算出所得颜色的各分量，最后返回拼合的颜色。下图即用此函数计算所得的颜色，从左到右f从0线性地变到1：

十三、根据迭代次数选择颜色的调色盘

回过头来看我们绘制Mandelbrot集合的程序，我们改写一下调色盘函数。

Java版本：

    // (8)调色盘
    int getColor(double d) {
        if (d >= 0) {
            return interpolation(d / MAXITERNUMBER, 0xFFFFFF, 0x202020);
        } else {
            return 0x000000;
        }
    }

    int interpolation(double f, int c0, int c1) {
        int r0 = (c0 >> 16) & 0xFF;
        int g0 = (c0 >> 8) & 0xFF;
        int b0 = c0 & 0xFF;
        int r1 = (c1 >> 16) & 0xFF;
        int g1 = (c1 >> 8) & 0xFF;
        int b1 = c1 & 0xFF;
        int r = (int) ((1 - f) * r0 + f * r1 + 0.5);
        int g = (int) ((1 - f) * g0 + f * g1 + 0.5);
        int b = (int) ((1 - f) * b0 + f * b1 + 0.5);
        return (r << 16) | (g << 8) | b;
    }

JavaScript版本：

    // (8)调色盘
    function getColor(d) {
        if (d >= 0) {
        	return interpolation(d / MAXITERNUMBER, 0xFFFFFF, 0x202020);
        } else {
            return 0x000000;
        }
    }

    function interpolation(f, c0, c1) {
        var r0 = (c0 >> 16) & 0xFF;
        var g0 = (c0 >> 8) & 0xFF;
        var b0 = c0 & 0xFF;
        var r1 = (c1 >> 16) & 0xFF;
        var g1 = (c1 >> 8) & 0xFF;
        var b1 = c1 & 0xFF;
        var r = Math.floor((1 - f) * r0 + f * r1 + 0.5);
        var g = Math.floor ((1 - f) * g0 + f * g1 + 0.5);
        var b = Math.floor ((1 - f) * b0 + f * b1 + 0.5);
        return (r << 16) | (g << 8) | b;
    }

我们得到

终于见到了海马尾和孔雀羽眼的形状，虽然还缺点颜色。

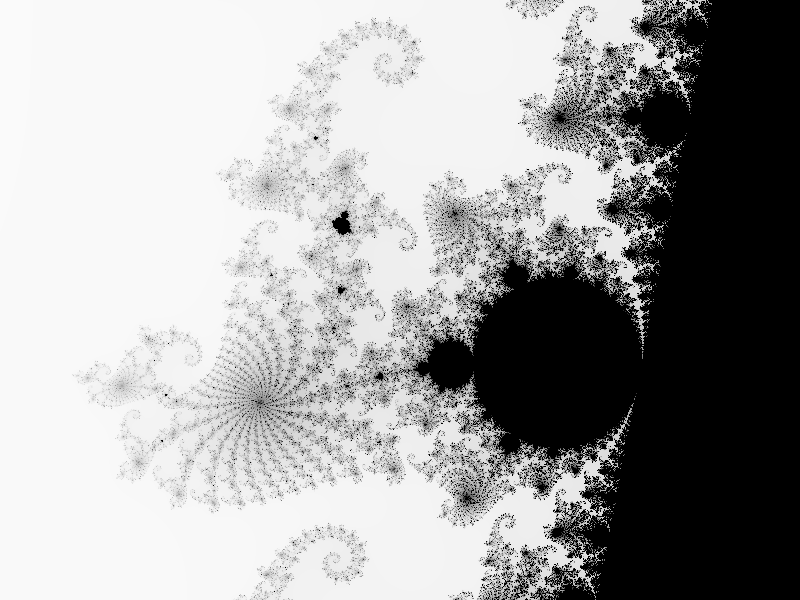
容易看出，上面新添的interpolation()函数计算的正是给定两颜色参数c0和c1的线性插值。而在新的调色盘函数getColor()中，我们不再作非黑即白的划分，而是根据超过逃逸半径所需的迭代次数（更精确地说，是根据“迭代次数/迭代次数上限”值，此值总是在0和1之间）来选择颜色：次数越少，像素的颜色就越靠近白色（十六进制数FFFFFF）；次数越多，像素的颜色就越靠近深灰色（十六进制数202020）。

和开始的非白即黑图相比，在新图中多出来的那些像素全都不是黑色，而是某种程度的灰色，也即代表它们的中心点都不属于Mandelbrot集合。所以在这里要纠正的一个误解，当我在前面说绘出的图是“Mandelbrot集合的图像”，这话并不精确。那些图像更象是Mandelbrot集合的图像再加上在Mandelbrot集合附近但并不属于Mandelbrot集合的点的某种结构的图像，而所谓的“某种结构”是通过对不同迭代次数的区别对待而显现出来的。

但反过来说，之所以在复平面的某个地方，不属于Mandelbrot集合的点会有复杂的结构，也是因为在那附近有属于Mandelbrot集合的点。粗略地说，一个点虽然不属于Mandelbrot集合，也就是在迭代过程中数列最终还是超出了逃逸半径，但是用了比其他点更多的次数，那是因为它比其他点更靠近Mandelbrot集合。此时虽然我们在取代表点的过程中没能直接取中属于Mandelbrot集合的点，但通过观测到离它很近的集合外的点，也算间接观测到了集合本身的形状。所以在这种意义下，我们说这个图像就是“Mandelbrot集合的图像”，也未尝不可。

当然，我们完全可以用其他的调色盘函数来取代前面举的例子。比如说换成（此处只提供Java版本，很容易改写成JavaScript版本）

    // (8)调色盘
    int getColor(double d) {
        if (d >= 0) {
            int q = (int) d % 3;
            if (q == 0) {
                return 0xFF0000;
            } else if (q == 1) {
                return 0x0000FF;
            } else {
                return 0x00FF00;
            }
        } else {
            return 0x000000;
        }
    }

这是以超过逃逸半径所需的迭代次数的除以3的余数来决定颜色。如果嫌细节部分乱糟糟，还可以分段考虑，迭代次数100以内（也即离Mandelbrot集合较远的那些点）考虑除以2的余数，超过100则用前面的线性插值，做到两种风格兼具：

    // (8)调色盘
    int getColor(double d) {
        if (d >= 0) {
            if (d <= 100) {
                int q = (int) d % 2;
                if (q == 0) {
                    return 0x0000FF;
                } else {
                    return 0x00FF00;
                }
            }

            return interpolation(d / MAXITERNUMBER, 0xFFFF00, 0xFF0000);
        } else {
            return 0x000000;
        }
    }

或者试试sin函数？

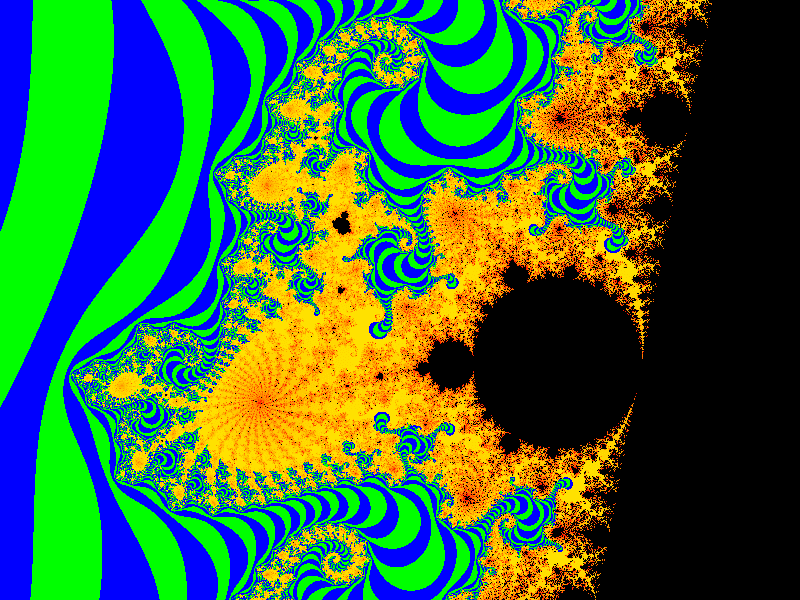
    // (8)调色盘
    int getColor(double d) {
        if (d >= 0) {
            return interpolation(Math.sin(d * 50), 0xFFFF00, 0xFF0000);
        } else {
            return 0x000000;
        }
    }

可能性无穷无尽。应该说这更是一个艺术问题或个人口味问题，已经和数学不太相关了。读者完全可以自己试着写调色盘函数，看看可以创造出什么样的画面来。