自绘Mandelbrot集合（六）

作者：安迁

十四、维基百科“放大”系列调色盘

前面提到过，在英文维基百科Mandelbrot集合条目中有一个“放大”系列，我觉得它很漂亮，所以想在这里模仿一下它的调色盘。

大家可以看到本文开头的三幅图像均在其内。

请把目前的程序源代码的第(8)部分完全替换为下面的代码： Java版本

    // (8)调色盘
    int getColor(double d) {
        if (d >= 0) {
            double k = 0.021 * (d - 1 + Math.log(Math.log(128)) / Math.log(2));
            k = Math.log(1 + k) - 29.0 / 400;

            k = k - Math.floor(k);
            k *= 400;
            if (k < 63.0) {
                return interpolation(k / 63.0, 0x000764, 0x206BCB);
            } else if (k < 167.0) {
                return interpolation((k - 63.0) / (167.0 - 63.0), 0x206BCB, 0xEDFFFF);
            } else if (k < 256.0) {
                return interpolation((k - 167.0) / (256.0 - 167.0), 0xEDFFFF, 0xFFAA00);
            } else if (k < 342.0) {
                return interpolation((k - 256.0) / (342.0 - 256.0), 0xFFAA00, 0x310230);
            } else {
                return interpolation((k - 342.0) / (400.0 - 342.0), 0x310230, 0x000764);
            }
        } else {
            return 0x000000;
        }
    }

    int interpolation(double f, int c0, int c1) {
        int r0 = (c0 >> 16) & 0xFF;
        int g0 = (c0 >> 8) & 0xFF;
        int b0 = c0 & 0xFF;
        int r1 = (c1 >> 16) & 0xFF;
        int g1 = (c1 >> 8) & 0xFF;
        int b1 = c1 & 0xFF;
        int r = (int) ((1 - f) * r0 + f * r1 + 0.5);
        int g = (int) ((1 - f) * g0 + f * g1 + 0.5);
        int b = (int) ((1 - f) * b0 + f * b1 + 0.5);
        return (r << 16) | (g << 8) | b;
    }

JavaScript版本

    // (8)调色盘
    function getColor(d) {
        if (d >= 0) {
            var k = 0.021 * (d - 1 + Math.log(Math.log(128)) / Math.log(2));
            k = Math.log(1 + k) - 29.0 / 400;

            k = k - Math.floor(k);
            k *= 400;
            if (k < 63.0) {
                return interpolation(k / 63.0, 0x000764, 0x206BCB);
            } else if (k < 167.0) {
                return interpolation((k - 63.0) / (167.0 - 63.0), 0x206BCB, 0xEDFFFF);
            } else if (k < 256.0) {
                return interpolation((k - 167.0) / (256.0 - 167.0), 0xEDFFFF, 0xFFAA00);
            } else if (k < 342.0) {
                return interpolation((k - 256.0) / (342.0 - 256.0), 0xFFAA00, 0x310230);
            } else {
                return interpolation((k - 342.0) / (400.0 - 342.0), 0x310230, 0x000764);
            }
        } else {
            return 0x000000;
        }
    }

    function interpolation(f, c0, c1) {
        var r0 = (c0 >> 16) & 0xFF;
        var g0 = (c0 >> 8) & 0xFF;
        var b0 = c0 & 0xFF;
        var r1 = (c1 >> 16) & 0xFF;
        var g1 = (c1 >> 8) & 0xFF;
        var b1 = c1 & 0xFF;
        var r = Math.floor((1 - f) * r0 + f * r1 + 0.5);
        var g = Math.floor ((1 - f) * g0 + f * g1 + 0.5);
        var b = Math.floor ((1 - f) * b0 + f * b1 + 0.5);
        return (r << 16) | (g << 8) | b;
    }

其中的interpolation()函数其实并未作变动，只是为了完整性重新给出一遍。

前一节中我说过，调色板的问题更是个艺术和口味问题，更何况我不是这个调色板的作者，所以为什么这个调色板是这么写的，我没法详细解释。这个调色板在“放大”系列的画面中表现相当出色，但在某些区域，尤其是棕黄色为主调的区域，就未必那么漂亮了。另外要提醒的是，这个调色板函数和“放大”系列使用的调色板并不完全一致，只是十分接近。

如果我们看调色板函数的主体部分

            double k = 0.021 * (d - 1 + Math.log(Math.log(128)) / Math.log(2));
            k = Math.log(1 + k) - 29.0 / 400;

            k = k - Math.floor(k);
            k *= 400;
            if (k < 63.0) {
                return interpolation(k / 63.0, 0x000764, 0x206BCB);
            } else if (k < 167.0) {
                return interpolation((k - 63.0) / (167.0 - 63.0), 0x206BCB, 0xEDFFFF);
            } else if (k < 256.0) {
                return interpolation((k - 167.0) / (256.0 - 167.0), 0xEDFFFF, 0xFFAA00);
            } else if (k < 342.0) {
                return interpolation((k - 256.0) / (342.0 - 256.0), 0xFFAA00, 0x310230);
            } else {
                return interpolation((k - 342.0) / (400.0 - 342.0), 0x310230, 0x000764);
            }

第一句先是对迭代次数作了一个线性变换，乘了一个系数0.021，使得颜色的变化不那么快。然后第二句主要是一个对数函数，使得颜色的变化更慢，它的一个作用是使得比如本文开始的第一幅图像中的每一个扇形中心能够有那种统一的明亮感。大家完全可以自己修改这些函数和参数来体会它们的作用。

接下去是k = k - Math.floor(k);，它使得颜色被重复轮流使用。被使用的则是后面if...else...条件语句中所提到的五种颜色和它们间的线性插值:

现在运行一下目前的程序：

在色调方面显然很象回事了，不过图像质量方面显然有很大问题。

###十五、抗锯齿

最明显的图像质量问题是有许多杂乱的点。产生这一现象的原因和字体以及游戏图像中物体边缘出现锯齿的原因差不多。比如下面左边的字体中，每个像素要么算作字体的一部分，颜色纯黑，要么算作字体外的部分，颜色纯白，那么在字体边缘必然产生锯齿现象。要减轻锯齿效应的话，就得进行抗锯齿处理。

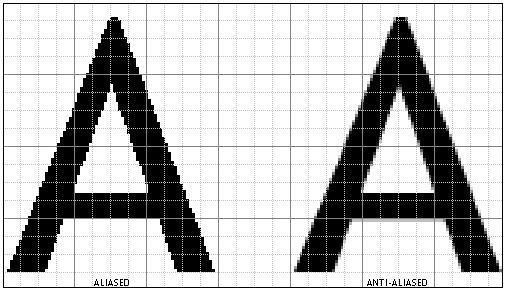
因为分形具有无限细节，在那些Mandelbrot集合边缘的那些像素内部有无限多的图形边缘，可是对每一个像素，我们却只以其中心点的计算结果来确定它的颜色，所以同样也会出现锯齿效应。这里我们将使用最暴力的超级采样法来处理这个问题。原理很简单：为一个像素我们多计算几个点，像素的颜色取这几个点颜色的平均。具体地说，原本我们只计算像素代表的正方形中点的颜色，现在将正方形划分成3x3的小正方形，并计算它们的中点的颜色，最后此像素的颜色为这9种颜色的平均：

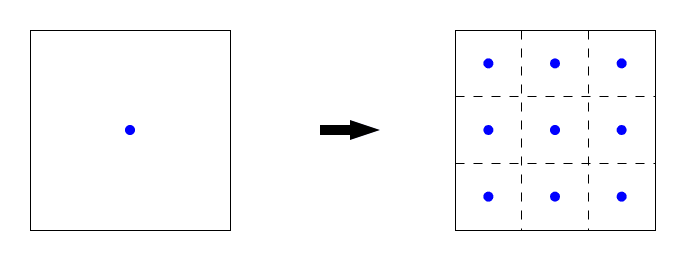
当然，现在计算量是原先的9倍。

于是将程序代码中的第(6)部分改成如下形式： Java版本

    // (6)计算颜色
    int calcColor(int col, int row) {
        double cx = (col - COFFSET) * PIXELSIZE + OX;
        double cy = (row - ROFFSET) * PIXELSIZE + OY;
        int r = 0;
        int g = 0;
        int b = 0;
        for (int i = -1; i <= 1; i++) {
            for (int j = -1; j <= 1; j++) {
                double d = iter(cx + i * PIXELSIZE / 3, cy + j * PIXELSIZE / 3);
                int c = getColor(d);
                r += (c >> 16) & 0xFF;
                g += (c >> 8) & 0xFF;
                b += c & 0xFF;
            }
        }

        r /= 9;
        g /= 9;
        b /= 9;
        return (r << 16) | (g << 8) | b;
    }

JavaScript版本

    // (6)计算颜色
    function calcColor(col, row) {
        var cx = (col - COFFSET) * PIXELSIZE + OX;
        var cy = (row - ROFFSET) * PIXELSIZE + OY;
        var r = 0;
        var g = 0;
        var b = 0;
        for (i = -1; i <= 1; i++) {
            for (j = -1; j <= 1; j++) {
                var d = iter(cx + i * PIXELSIZE / 3, cy + j * PIXELSIZE / 3);
                var c = getColor(d);
                r += (c >> 16) & 0xFF;
                g += (c >> 8) & 0xFF;
                b += c & 0xFF;
            }
        }

        r /= 9;
        g /= 9;
        b /= 9;
        return (r << 16) | (g << 8) | b;
    }

注意到对颜色取平均必须是分别对红绿蓝三个分量取平均，再拼合成最终的颜色。

运行程序，得到以下图像（注意运行时间大约为前面的9倍）：

很接近我们最终希望得到的结果了。

参考文献：

[1] 维基百科Mandelbrot set条目 https://en.wikipedia.org/wiki/Mandelbrot_set