数学科普

自绘Mandelbrot集合（四）

作者：安迁

十、非黑即白

让我们把Java版本中的(7)和(8)部分换成下面的代码：

// (7)迭代计算
    double iter(double cx, double cy) {
        double x = 0;
        double y = 0;
        double newx;
        double newy;

        double smodz = 0;
        int i = 0;
        while (i < MAXITERNUMBER) {
            newx = x * x - y * y + cx;
            newy = 2 * x * y + cy;
            x = newx;
            y = newy;
            i++;

            smodz = x * x + y * y;
            if (smodz >= ESCAPERADIUS) {
                return i;
            }
        }

        return -1.0;
    }

    // (8)调色盘
    int getColor(double d) {
        if (d >= 0) {
            return 0xFFFFFF;
        } else {
            return 0x000000;
        }
    }

相应的JavaScript版本为

    // (7)迭代计算
    function iter(cx, cy) {
        var x = 0;
        var y = 0;
        var newx;
        var newy;

        var smodz = 0;
        var i = 0;
        while (i < MAXITERNUMBER) {
            newx = x * x - y * y + cx;
            newy = 2 * x * y + cy;
            x = newx;
            y = newy;
            i++;

            smodz = x * x + y * y;
            if (smodz >= ESCAPERADIUS) {
                return i;
            }
        }

        return -1.0;
    }

    // (8)调色盘
    function getColor(d) {
        if (d >= 0) {
            return 0xFFFFFF;
        } else {
            return 0x000000;
        }
    }

运行得到以下图像

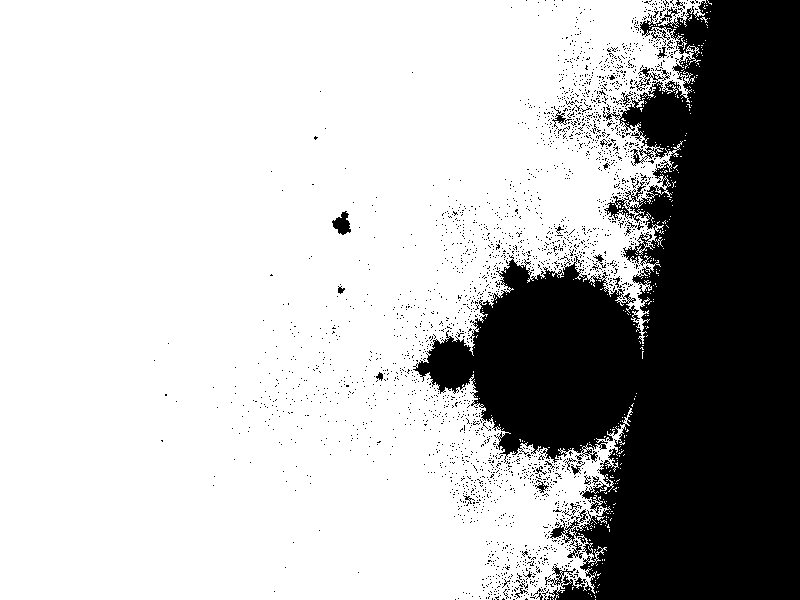
-0.743030 + 0.126433i @ 0.016110 /0.75
-0.743030 + 0.126433i @ 0.016110 /0.75

看上去我们的确绘出了某种正确的东西，因为右边那个大虫子头很像前面我们在Mandelbrot集合上看到的那些。如果和本文开始的第三幅图像比较区域坐标和图像，就会发现这是同一块地方。可为什么我们现在画出的这幅图像里没有那些漂亮的象海马尾巴的螺旋，和类似孔雀尾羽上“眼睛”的图案呢？多出来的是一堆杂乱的黑点。

先让我们来复习一下Mandelbrot集合的定义和性质。对一个复数c，它属于Mandelbrot集合，当且仅当下面这个递归定义得到的无穷复数列一直处于复平面上以原点为中心以2为半径的圆内： z0 = 0; zn = zn-12 + c; 如果我们把zk写成xk+yki这样实部和虚部分开的形式，同样也把c写成cx+cyi的形式（cx和cy分别为c的实部和虚部），那么上面的递归定义其实就是 x0 = 0， y0 = 0； xn = xn-12 - yn-12 + cx, yn = 2xn-1yn-1 + cy 复数cx+cyi属于Mandelbrot集合，当且仅当对所有的自然数n，xn2+yn2 < 22 = 4。

于是很容易看出，上面给出程序的迭代计算部分实际上就是在实际计算这些xn和yn。由于Mandelbrot集合定义的简单性，可称为我们这个程序的核心算法部分，只有区区二十来行：

// (7)迭代计算
    double iter(double cx, double cy) {
        double x = 0;
        double y = 0;
        double newx;
        double newy;

        double smodz = 0;
        int i = 0;
        while (i < MAXITERNUMBER) {
            newx = x * x - y * y + cx;
            newy = 2 * x * y + cy;
            x = newx;
            y = newy;
            i++;

            smodz = x * x + y * y;
            if (smodz >= ESCAPERADIUS) {
                return i;
            }
        }

        return -1.0;
    }

当然我们不可能真的把整个无穷数列都算出来，所以我们必须定一个迭代次数的上限MAXITERNUMBER（可调参数，目前它的值为1000），如果算了这么多次后，数列的各项还是没能跑出逃逸半径，也就是说xn2+yn2 < ESCAPERADIUS（这里ESCAPERADIUS也是一个可调参数，即逃逸半径的平方，目前它的值是4），那么我们就算这个点在Mandelbrot集合里了。所以上面这个迭代计算函数的意思就是：如果迭代若干次后数列出了逃逸半径，返回首次出逃逸半径时的迭代次数；如果迭代了MAXITERNUMBER次数列还是没出逃逸半径，那么返回-1.0。而第(8)部分调色盘函数则将返回-1.0的那些点画成黑色（颜色代码为十六进制整数000000），其他情况画成白色（颜色代码为十六进制整数FFFFFF）。这是一种非黑即白的染色画法，我们在画面上看到的黑色部分就是Mandelbrot集合。

除去不可避免的浮点数计算精度问题，这样的方法还有两个无可奈何的缺点。首先它肯定会把一些不属于Mandelbrot集合的点算在其内，因为有个迭代次数的上限。算1000次数列各项还在逃逸半径内，保不准再算下去第1001次或者第10000次就出去了。我们当场就可以试一试，把“(1)可调参数”这部分中的迭代次数上限MAXITERNUMBER改成10000再运行，就得到了

-0.743030 + 0.126433i @ 0.016110 /0.75 迭代次数上限10000次
-0.743030 + 0.126433i @ 0.016110 /0.75 迭代次数上限10000次

如果把MAXITERNUMBER改成100000，则有（允许的迭代次数多了，计算时间也必定相应增加。所以如果尝试100000次的话，取决于你使用的电脑性能，也许要耐心等几分钟）

-0.743030 + 0.126433i @ 0.016110 /0.75 迭代次数上限100000次
-0.743030 + 0.126433i @ 0.016110 /0.75 迭代次数上限100000次

可以看出，随着迭代次数上限的增加，杂点越来越少。可问题是，用增加迭代次数上限的方法只能去除“假点”，那些海马尾和孔雀羽眼不会因之而出现。

这就要谈到上面方法的第二个缺点。在第九节中我们已经提到过，一个像素是被它的中心点代表的，它的颜色完全由这个像素所代表的正方形的中心点的性质决定。在本节“非黑即白”的画法下，如果这个正方形里有许多Mandelbrot集合的点，但是不幸它的中心点不在其内，那么这个像素也会被画为纯白。

在前面这几幅黑白图中，我们都能在画面中心偏左上处看见一个小虫子，它是Mandelbrot集合的一部分，看起来孤零零地远离右侧的大的黑色部分。但数学家们早已证明，整个Mandelbrot集合是连通的，也就是说，这个小虫子是和整个Mandelbrot集合连为一个整体的。只是由于我们绘图算法的缺陷，才被画成孤岛的样子。

如果你试验了修改参数MAXITERNUMBER的结果，请将其改回1000次，我们暂时只需要不高的迭代次数上限，以节省计算时间。

<（三）
（五）>