关于围绕数大于等于5的拼块的注记

在《Voderberg拼块的妙用：围绕数为2的拼块》中我提到“对于大于等于3的自然数n，我们都容易找到围绕数为n的拼块。（不过这个“容易”也是相对的，比如说，大家可以找找围绕数为5的拼块，并不那么容易。）”。后来我在网上找了找相应的文献，没找到有专门讲这个问题的。所以虽然鸡毛蒜皮，我觉得还是写一个注记为好，免得说话无据。

围绕数为2，3和4的拼块已经在上面所说的文章中举过例子。下面我给出一个对任意大于等于6的自然数n，构造围绕数为n的拼块的方法。关于围绕数为5的拼块则单独在后面描述。

一、n>5

对任意大于5的自然数n，令m=n-4，我们构造下面这样由若干个带凹凸的2*1的长方形组合起来的拼块，其中水平方向带凹的长方形有m个（下图的m=4，也即n=8)：

容易看出，那些凹只能用那个凸来拼嵌，反之亦然。要用这个拼块来围绕它自己，下面这几块是必须的，位置是固定的：

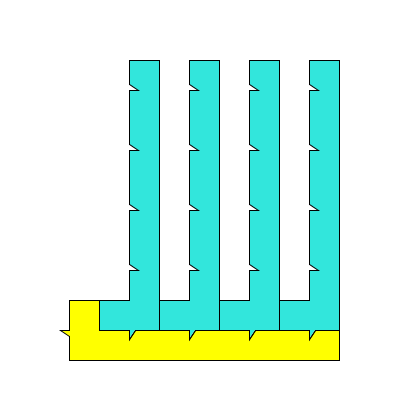
黄块左方的凸必须由一个凹来拼嵌，下图中我们选择最上边的这个凹。

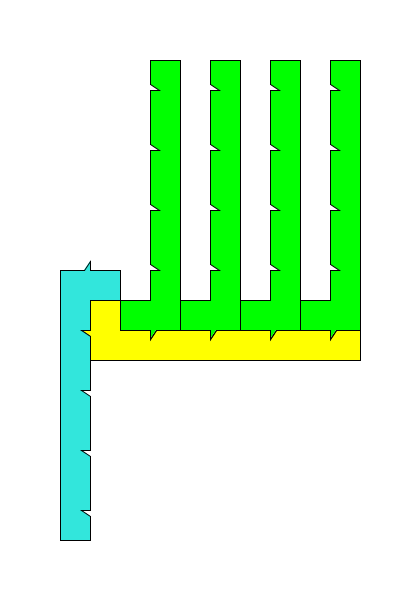
这样还有一点露出，需要另一块来遮住。容易看出，如果我们不选这第一个凹，而是用下面其他凹来拼黄块上的凸，黄块上方长度为1的边就会露出来，需要有长度大于1的直边来盖住。可是很容易看出剩下的空间不足以放进去这样一条长边。所以图3放置这块的位置其实也是固定的，再加上完全盖住剩下角落的这块：

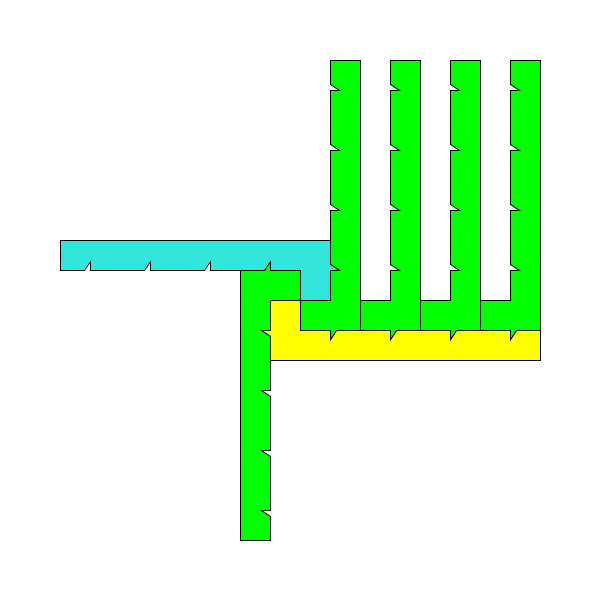
黄块下方的长边要另一块来围住。右边短边虽短，也还需一块：

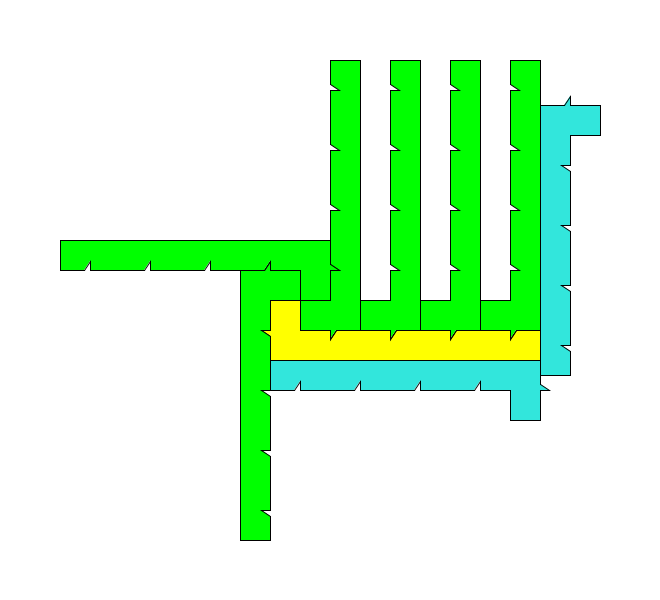
具体到上图，m=4，这正是一个围绕数n=8的拼块。对m>1的自然数来说，这个构造围绕数为n=m+4的拼块的方法都是可行的，比如下面给出的m=2（n=6）和m=10（n=14）时的情形：

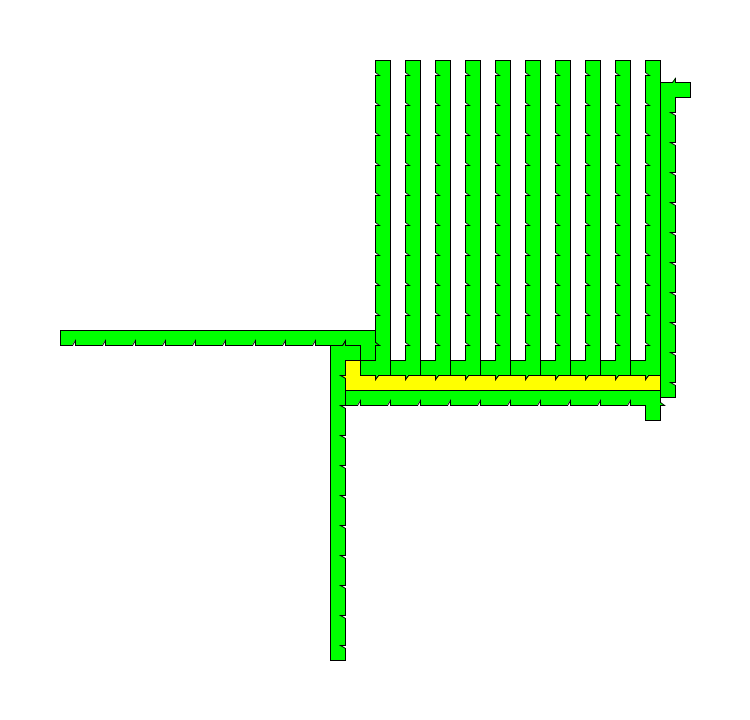
现在我们知道为什么开头取m=n-4了。图2加的那m块可以随m变化而变化，再加上图3到图5加上的不以m变化而变化的4块，得到围绕着原拼块的m+4=n块拼块。而且我们证明了这是最少的块数，于是拼块的围绕数为n。

那为什么m=1（n=5）时这个方法不灵呢？因为在左下角会出现不能严丝合缝围绕住的局面，结果还是需要6块：

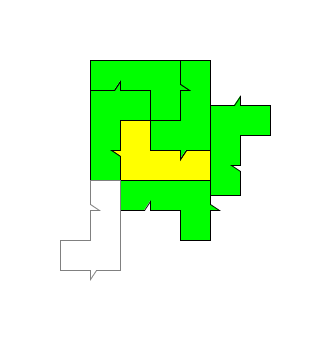
二、n=5

所以对于围绕数为5的拼块我们必须另辟蹊径，好在这也不难。考虑下面由三个加了凹凸的正方形组合起来的拼块：

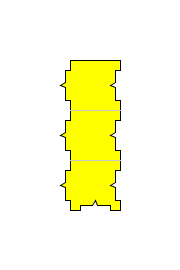
这个凹凸的具体形状并不一定要严格象我画的这样一个细长条加一小尖，只是要注意两件事：一是形状必须足够特殊使得只能用凹来拼凸凸来拼凹，二是使得这个拼块的左右两边没有长度大于原正方形边长的直线部分。这样我们至少需要5个拼块（也只需5个拼块）来围绕一个拼块：

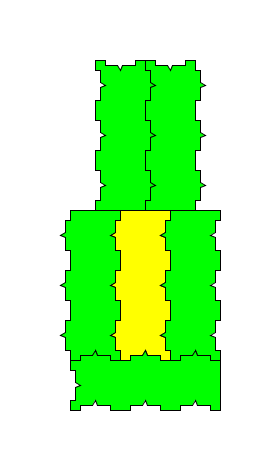
三、附记

科学公园的编辑在收到我的初稿后，希望我能补充一下想到这个结果的过程。我就简单地说一下。

要得到一个对于较大以至于非常大的n都能成立的围绕数为n的拼块的构造方法，马上能想到的就是它的边缘不会是简单的长直线，那样其他拼块围绕它的时候也无需很多副本，只使用它们同样拥有的长直边就行了。如果将（一）中的拼块的凹凸去掉，无论它多长，它的围绕数总是4：

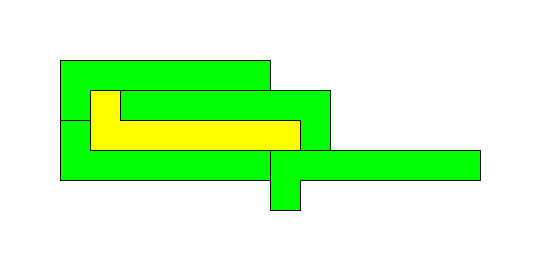
能够满足我们需要的拼块应该是这样的：它的上面有许多个特别形状的部位需要拼嵌，可是能拼嵌进这个形状的部位，每个拼块却只有一个。于是为了围绕一个拼块，就需要很多拼块。最简单的此类拼块是一根直杆上有许多凹槽，却只有一个突起：

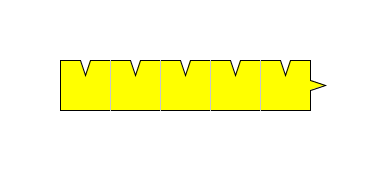
从某种意义上来说，它的确能完成任务：

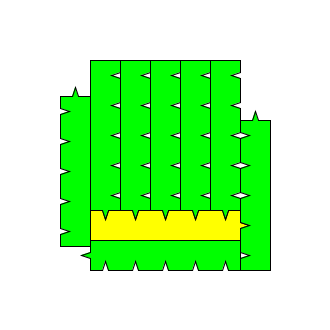
除了最左最右和下面3块是常规不变的外，上面那一族拼块的数目和一块拼块上的凹槽数相同。对照前面L形拼块的n=m+4的公式，这种拼块的公式有类似的n=m+3的形式，不过m必须大于2。

但我们可以看到，这样的围绕造成了许多不和外界连通又不被拼块覆盖的小洞。在此类研究中，成文或半成文地，这样的局面是不被允许的。所以为了避免造成这种情况，我考虑到了前面的L形拼块，它可以拉开这些“枝杈”的距离，使得凹部形成的空隙不至于和外部脱开。另外我将L形拼块的凹凸部改成了不对称的形状，这样拼嵌的时候就不用考虑拼块的正反了（也许大家注意到了，在图11中有些拼块是原拼块的镜像，而不能仅由原拼块平移和旋转得到），凹和凸拼嵌起来只能有一种方式，证明的叙述也相应变得简单。