数学科普
自绘Mandelbrot集合(二)
作者:安迁
三、专业软件
首先,如果你的目的只是绘制Mandelbrot集合的图像,而不在乎了解其中的具体原理,那么我推荐你使用专门的分形绘制软件。这些软件有绘制多种分形的能力,大量可自定的设置,更快的运行速度,其开发人员也有多年分形绘图的专业知识。我要在这里介绍的区区一百五十行程序,无论在功能和性能上,都不可能与之相比。你可以在网上搜索引擎中寻找这些软件,也可参照参考文献中维基百科Fractal-generating software条目。有兴趣的朋友可以注意一下其中两个软件。
一是Kalles Fraktaler,这是一款开源软件,放大功能极其强大。前面提到分形的特征是自相似,无论放大多少倍,都能在那个尺度找到和整个集合相似的局部。于是网上有一些分形爱好者制作了不少“深度放大”视频,从整个Mandelbrot集合开始不断放大某个局部。有人使用Kalles Fraktaler制作了放大倍数高达1010000的视频,这意味着如果最终的画面大小是1毫米边长,那么按这个尺度把最初的Mandelbrot集合整个显示出来的话,画面边长会约是109981光年。而可观测宇宙的直径,也只不过是约1000亿也即1011光年。
二是Ultra Fractal,可以免费试用的商业软件。它的各项功能都极其强大,是分形绘制的专业软件。本文中试图模仿风格的英文维基百科Mandelbrot set条目中“放大”系列的十几幅图像,就是一位叫Wolfgang Beyer的德国物理学家使用Ultra Fractal软件绘制出来的。
如果你愿意了解一下Mandelbrot集合图案绘制的原理,那么就请继续阅读本文。
四、区域坐标和点彩绘图
为了确定我们要绘制的图形区域,必须先介绍区域坐标这个概念。一个复平面上的点可以由一个复数来定义,也即两个实数,分别是此复数的实部和虚部。我们用这样两个实数OX和OY来表示要绘制的区域的中心点。还需说明所绘制区域的大小,我们用一个实数WIDTH来说明此区域的宽度,而用另一个实数RATIO来说明此区域的高宽比。这四个参数完全确定了一个复平面上长方形区域,它的中心点在复数OX+OYi处,宽WIDTH,高WIDTH*RATIO。这就是这个区域的坐标。本文中我们用“OX + OYi @ WIDTH /RATIO”这样的形式来表示区域坐标。比如本文第一幅图像下的标注“-0.7436438885706 + 0.1318259043124i @ 0.0000000041493 /0.75”即是说,这幅图形所绘的Mandelbrot集合局部区域在复平面上的中心点位于-0.7436438885706 + 0.1318259043124i,宽度为0.0000000041493,高宽比3/4。
在本文大部分我自绘的图像下,我都标出了它所绘的区域坐标,以便读者查询验证。
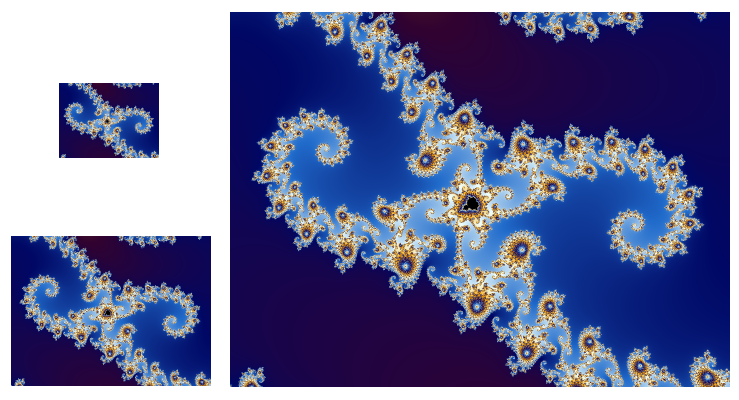
要指出的是,区域坐标和最终绘出的图像的高宽比是一致的,但区域坐标和最终绘出的图像的大小(图像的宽度,也即横向的像素数)是无关的。图像的宽度是一个整数,而区域的宽度则是一个实数(通常远远小于1)。同一个区域坐标用不同宽度的图像绘制,画出来的总是Mandelbrot集合的同一个地方,只不过宽度越大,图像就越清晰,当然绘制时间也和此值的平方成正比。比如下面三幅图像绘制的都是同一区域坐标的图像,但宽度分别为100、200和500像素。
Mandelbrot集合的绘制原理则很简单,用短短一段话就可以概括:
“如何画一幅宽为w个像素,高为h个像素的图像?只要为每个像素计算一下它该是什么颜色,然后在相应位置画上这种颜色,画完所有w*h个像素,图像就绘制完成了。”
这话的风格听起来有点象那个笑话:“如何把大象装进冰箱?把冰箱门打开;把大象放进去;把冰箱门带上。”不过我们从中至少可以知道,为了编制此程序,在具体画图的方面我们只要了解如何在所使用的计算机语言里画点就可以了,而不需要了解如何画直线、曲线或色块。这种画法有点类似于绘画中新印象主义,或称点彩画派的风格,只是我们将要使用的颜色种类要多得多。这同样也大大降低了把程序从一种语言移植到另一种语言的难度;因为在不同语言间,普通的整数和浮点运算甚至是流程控制的的写法的区别通常不大,但在画图的编程接口方面则往往区别相当大。
文章接下去的几节将要引入能运行却什么都不干(其实还是能画出一个红色长方形来)的程序代码,大概是本文中最没有意思的部分。不过虽然大家都想看的其实只是把大象装冰箱的第二步,但毕竟打开和关上冰箱门也是必不可少的步骤,不能不做。
五、开发工具准备
从理论的角度来看,Mandelbrot集合的绘制原理并不依赖所使用的计算机语言。只要是一门能够进行一定精度的浮点运算,并且能够点彩也即在指定位置的像素上绘制指定颜色的语言(所有的实用计算机语言大概都有这样的功能),都可以运用这个原理来绘制Mandelbrot集合图像。但实际上介绍程序编制的文章常有的一个尴尬之处,就是要选定具体的编程语言,一下子就把无法或懒得使用这种语言的许多人挡在门外。本文也不能避免这点。
我在这里选择的第一门语言是Java。首要原因是我对它比较熟悉;其次它也被相当广泛地运用,所以熟悉的人也比较多。但编译和运行Java程序必需安装一些开发工具如JDK,如果平时就在电脑上使用Java的人要尝试我的Java版程序没有问题,没有这些开发工具的朋友就比较麻烦。而我也无意在此介绍如何编译运行Java程序,只假设要尝试Java代码的朋友已经知道这些事情如何做了。
所以我同时也给出内嵌JavaScript程序的HTML页面源码。这样你只要打开一个文本编辑器,拷贝粘贴我给出的源码,存成后缀为html的文件,再用网络浏览器打开即可运行程序。一般流行的较新版本的网络浏览器均可,如Chrome,Firefox或Internet Explorer等等,推荐使用Chrome。为了只需要解释一次代码,我将JavaScript代码写得尽量类似Java版本的,结果就是写出的JavaScript代码充满了浓厚的Java味道,而且做了一些无用功,比如整数的颜色代码和它的红绿蓝分量之间没有必要地互相转换。同时我无意使用面向对象的编程,一来许多计算机语言并不支持面向对象的编程,二来实现它的语法在Java和JavaScript中有很大不同,会使两套程序的区别没有必要地增加。说到底,这里给出的程序源码只是一个例子,目的是说清原理并能很快试用。如果你想要实际地应用它,必须进行深刻的改写和重构。
参考文献:
[1] 维基百科Mandelbrot set条目 https://en.wikipedia.org/wiki/Mandelbrot_set
[2] 维基百科Fractal-generating software条目https://en.wikipedia.org/wiki/Fractal-generating_software