自绘Mandelbrot集合（一）

本文介绍如何用计算机程序绘出与下面图像类似的分形图案。程序实例将以Java语言和内嵌JavaScript程序的HTML文件两种形式给出，最终的程序量不超过150行，移植到其他常用的计算机语言上应当也是容易的。本文也适当介绍必要的关于Mandelbrot分形的知识。

一、Mandelbrot集合

Mandelbrot集合大概是最有名的分形了。

分形是一种具有自相似性质的空间点集，也就是说，在任何一个比它自身小的空间尺度上，都能找到它的某些局部，和它本身看起来是差不多的。以Mandelbrot集合为例，它是复平面上的一个点集，整体看起来是这个样子（黑色部分）

我们可以看到，它本身长得象个大虫子，它的边缘上又附着着无数个大大小小的虫子头部。本文开始的第二幅图中，有一个和Mandelbrot集合本身长得很象的虫子，但那已经是上图中一个叫“海马谷”的地方放大二十万倍后的图像了。

Mandelbrot集合的图像看起来很复杂，但它的定义却极其简单。

随便取一个复数c，让我们来考虑下面的递归定义得到的无穷的复数列： z₀ = 0; z_n = z_n-1² + c; 如果这个数列各项的绝对值（或者叫模，也即一个复数在复平面上距0点的距离）一直局限于一个有限的区域（事实上可以证明，这个区域只要取和0点距离小于2这个圆形区域即可），那么c就属于Mandelbrot集合；反之，如果这个数列中的项会跑出任意指定的有限区域去（实际上只需跑出上述圆形区域），则c不属于此集合。

比如取c=1，我们就有 z₀=0, z₁=1, z₂=2, z₃=5, z₄=26, z₅=677, z₆=458330, z₇=210066388901 …… 看样子这个数列会越来越大，离0点越来越远，所以1不属于Mandelbrot集合。

如果取c=-1，我们有 z₀=0, z₁=-1, z₂=0, z₃=-1, z₄=0 …… 显然这个数列以后会在0和-1间跳来跳去，所以-1属于Mandelbrot集合。事实上，-1就是上图中虫子头部，也就是左边那个大圆的圆心。

如果取c=i，我们有 z₀=0, z₁=i, z₂=-1+i, z₃=-i, z₄=-1+i, z₅=-i …… 显然这个数列以后会在-i和-1+i间跳来跳去，所以i属于Mandelbrot集合。

如果取c=-1/2+1/2i，我们有 z₀=0, z₁=-1/2+1/2i, z₂=-1/2, z₃=-1/4+1/2i, z₄=-11/16+1/4i, z₅=-23/256+5/32i, z₆=-33839/65536+1933/4096i, z₇=-1958946911/4294967296+1698077/134217728i …… 看样子这个数列各项的实部和虚部的绝对值都不会超过1，不会远离0点。所以-1/2+1/2i属于Mandelbrot集合。

而取c=1/2-1/2i，我们有 z₀=0, z₁=1/2-1/2i, z₂=1/2-i, z₃=-1/4-3/2i, z₄=-27/16+1/4i, z₅=841/256-43/32i, z₆=621713/65536-38211/4096i …… 看样子这个数列各项的实部和虚部的绝对值都越来越大，离0点越来越远。所以1/2-1/2i不属于Mandelbrot集合。

数学家们对Mandelbrot集合的兴趣始于一门从二十世纪初发展起来的名为复动力系统的数学分支。法国数学家Adrien Douady等人在80年代对它进行了深入的研究，并以分形之父，美国数学家Benoît Mandelbrot的名字为之命名。

二、图像

Mandelbrot集合的图像因它洛可可式繁复卷曲华丽的风格而受到大众的欣赏和赞叹，与其他分形图案一起，是许多艺术家和设计师的灵感来源。当我在屏幕上画出本文开始的第一幅图像时，太座在旁边看见了就说：“如果印在丝巾上应该很漂亮。”

关于Mandelbrot集合的图像，最早公开发表大概是在1978年Robert Brooks和Peter Matelski的一篇论文中。Mandelbrot本人则是在1980年3月在其任职的IBM Thomas J. Watson研究中心里第一次一睹其真容。

而大众对Mandelbrot集合的兴趣，很大程度上是由《科学美国人》1985年八月号Alexander Dewdney的专栏文章引起的。笔者也是在1980年代末看到此期《科学美国人》，被封面和文中的Mandelbrot集合图像吸引得目眩神迷。这篇文章现在可以在《自然》杂志网站上免费下载，链接请参见参考文献。

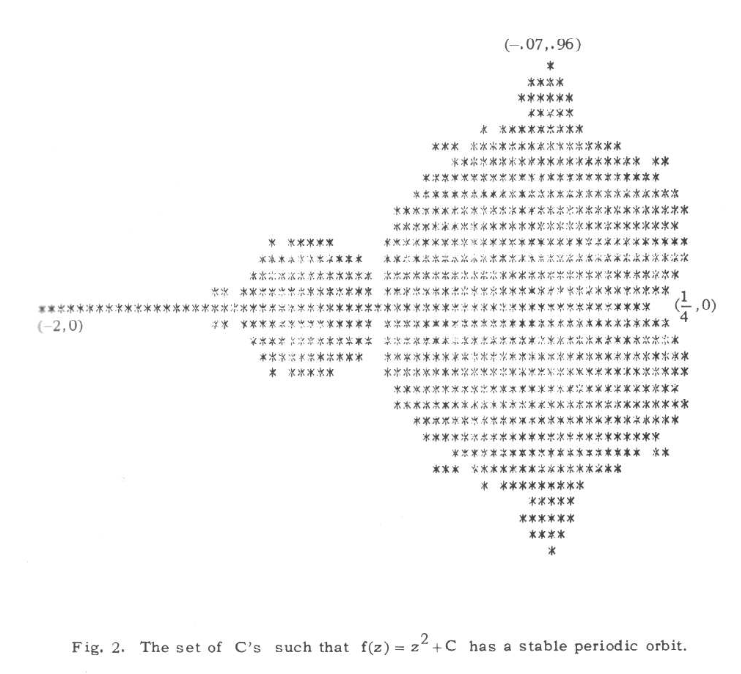
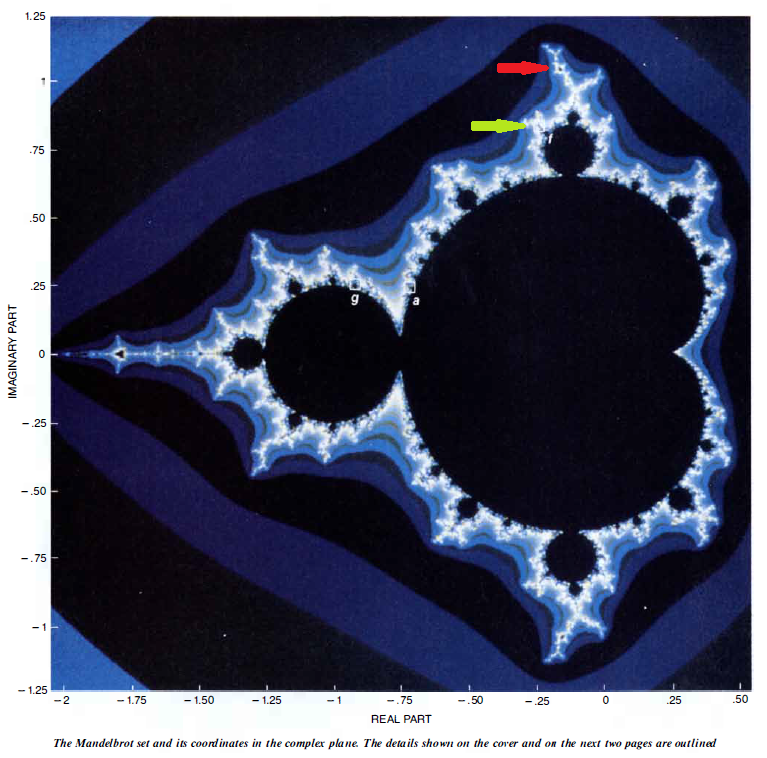
顺便说一句，《科学美国人》的这篇文章里f图在整个Mandelbrot集合图像中的位置标记是错误的。它的实际位置应该在下图红色箭头所标记的位置，而非绿色箭头所指的标为f的白色方框处。笔者查找了文中那几个图像的位置，但无法在指定位置发现和f图相同的区域，花了约半小时才意识到这个错误，故特此记之。

当然，我们看到的Mandelbrot集合的华美图案，是和强大的计算能力密切相关的。从今天的标准来看，本节中所说的这些图像显然有些粗糙了；而本文的目标就是告诉大家如何自己动手，画出更漂亮的Mandelbrot集合图像来。正是由于今天个人电脑计算能力的强大，才有可能让我们在家中就能绘出从前只有在世界级研究中心里才能见到的绚丽图案。

---

参考文献：

[1] Robert Brooks and J. Peter Matelski, The dynamics of 2-generator subgroups of PSL2(C), Annals of Math. Studies, Princeton, no.97, pp. 65–72 (1981).

[2] Alexander Dewdney, A computer microscope zooms in for a close look at the most complicated object in mathematics. Scientific American, no.253, pp.16–24 (1985) 下载地址： http://www.nature.com/scientificamerican/journal/v253/n2/pdf/scientificamerican0885-16.pdf

[3] 维基百科Mandelbrot set条目 https://en.wikipedia.org/wiki/Mandelbrot_set