数学科普
边看边说序列的宇宙学(七·完)
作者:安迁
十、加强版算术定理
因为前面所说的那些形式的Perron–Frobenius定理都不能应用于边看边说矩阵M,于是康威就在论文中用直观的方法证明了一个猴版的结论,也就是前面介绍的算术定理。之所以称它是“猴版”,是因为其结论是不完全的。它只是说,从任何一个普通化合物开始,每一步演化得到的数字串的长度和上一步相比,越来越趋近于康威常数λ,却没有对演化n天后的数字串的长度作直接的估算。下面这幅11钠,29铜和62钐开始演化后30天内序列中数字串长度的统计图很直观地显示了这个定理的正确性。注意到图中纵轴是对数坐标轴,指数函数在这样的坐标系中的图像是直线。随着项数的增长,图中的三条曲线很快都近似直线。三条直线的斜率都一样,通过算术定理我们知道这斜率就是康威常数λ。
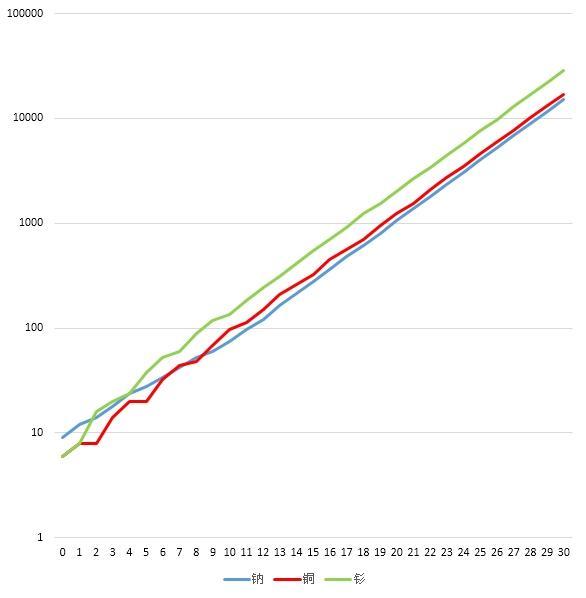
但是算术定理无法说明的是,三条直线高低不同的位置是由什么决定的。如果把三条直线所对应的指数函数写成y=cλn的形式,我们就要问:对于每种不同的普通化合物,它所对应的c是由什么决定的,如何计算呢?下面的表中,我们对若干项n计算了以上述三种普通元素开始的边看边说序列的“演化n天后数字串的长度/λn”的值,也即上述c的经验值:
| 演化天数 | 11钠 | 29铜 | 62钐 |
|---|---|---|---|
| 0 | 9.0000000 | 6.0000000 | 6.0000000 |
| 1 | 9.2054382 | 6.1369588 | 6.1369588 |
| 2 | 8.2386201 | 4.7077829 | 9.4155658 |
| 3 | 8.1257259 | 6.3200090 | 9.0285843 |
| 4 | 8.3112075 | 6.9260063 | 8.3112075 |
| 5 | 7.4383076 | 5.3130769 | 10.094846 |
| 6 | 6.9288035 | 6.5212268 | 10.596994 |
| 7 | 6.5658633 | 6.8785235 | 9.3798047 |
| 8 | 6.2360432 | 5.7563475 | 10.553304 |
| 9 | 5.5197606 | 6.2557287 | 10.855529 |
| 10 | 5.2223254 | 6.7749087 | 9.5977873 |
| 20 | 5.2991480 | 6.1258948 | 9.9309221 |
| 50 | 5.2985020 | 6.0506340 | 10.037356 |
| 100 | 5.2993912 | 6.0503887 | 10.035343 |
| 1000 | 5.2993903 | 6.0503907 | 10.035341 |
| 10000 | 5.2993903 | 6.0503907 | 10.035341 |
| 100000 | 5.2993903 | 6.0503907 | 10.035341 |
看来,与11钠,29铜,62钐相对应的c值应该分别大约是5.2993903,6.0503907和10.035341。29铜和62钐的长度都是6,可是对应的c值却差许多;11钠的长度是9,可是对应的c值却反而小于29铜和62钐的。也就是说,从两个初始长度相同的化合物出发,接着用相同时间演化出来的化合物长度可以差许多,甚至有可能初始长度长的化合物,接下去演化出来的化合物的长度反而短。算术定理无法告诉我们这是为什么,更不能对每种化合物预言和它对应的c值。
康威的论文写于1980年代。二十多年后,代数学家们对Perron–Frobenius定理的研究更加深入,与其说现在我们有Perron–Frobenius定理,不如说我们有Perron–Frobenius理论,我们拥有了当年康威所没有的工具。文献[2]中的定理2.4简直就是为边看边说矩阵M量身定造的。它说,如果一个n阶实系数正方矩阵A有一个绝对值最大的正特征值,而且和它相关的左右特征向量都可以取分量非负的话,那么前面Perron–Frobenius定理中所叙述的“当自然数n趋向于无限时,矩阵序列{(1/μn)An}的极限是矩阵vw”的结论同样成立。
注意到在原版Perron–Frobenius定理中,关于存在绝对值最大的正特征值以及正分量的左右特征向量的命题,是结论的一部分,在上面的定理中则成了条件的一部分。对于矩阵M,这个条件是可以独立计算和验证的。关于矩阵的特征多项式、特征值和特征向量的理论,是线性代数的基础知识,在此我就不重复了。
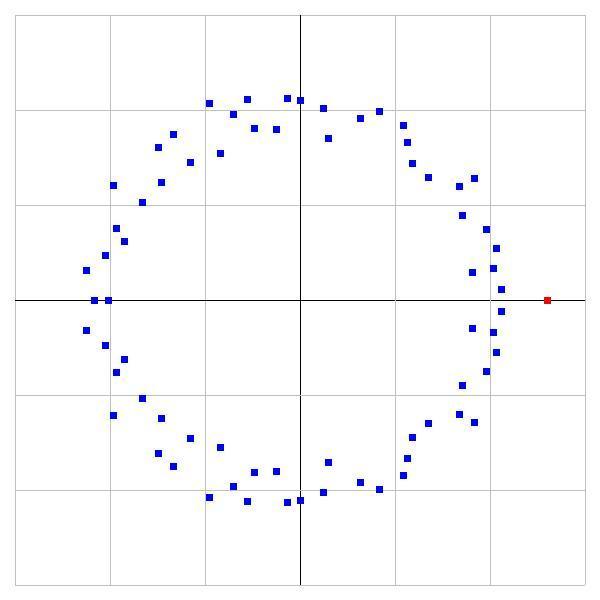
康威证明了,M的92次的特征多项式可以被因式分解,去掉那些根为0或±1的因子,剩下的就是我们在算术定理中看到的那个71次多项式。下图是这个多项式的解的图示,最右方红点即康威常数λ。
在这里值得一提的是幂法求特征值的迭代算法(具体方法可以以“幂法 特征值”为关键词在网上查询)。本来这个算法有点鸡肋,因为它只能求绝对值最大的特征值(如果改变一下也可求绝对值最小的特征值,称为反幂法),所以如果要求所有的特征值就不适用了。可是这里我们恰恰只需要求绝对值最大的特征值,用求所有特征值的算法求出一堆特征值来到反而还得另去筛选出绝对值最大的来,反而麻烦。而且幂法能同时求出这个特征值和相关的特征向量。这简直是要睡觉就有人送上了枕头!笔者用这个方法轻松地就求出了M这个绝对值最大的特征值小数点后三百位的值和精确程度类似的相应的特征向量,虽然这么精确的数据其实没什么大用处。
于是我们就有了比原版算术定理更强的 (加强版算术定理) 1) 边看边说矩阵M有一个在其所有特征值中绝对值最大的特征值λ。λ为正实数,是M的特征多项式的单根。 2) M有一个关于λ的,分量都是正实数的,分量之和为1的(右)特征向量v,我们称v为丰度向量。 3) M有一个关于λ的,分量都是正实数的左特征向量w,满足wv=1。我们称w为富度向量。 4) 当自然数n趋向于无限时,矩阵序列{(1/λn)Mn}的极限为矩阵vw。
事实上定理中的λ就是康威常数λ。在原版定理中它是一个神秘的71次多项式的根;而在加强版定理中,它被明确为边看边说矩阵的唯一的绝对值最大的特征值。下面我们来看看如何由上述加强版定理推导出原版算术定理。
注意到在文献[2]定理2.4中,v并不是被唯一确定的,而是可以被乘以任意一个正实数,而在上述加强版定理中,对丰度向量v有一个“分量之和为1”的附加要求,v就被唯一确定了。正如它的名字所暗示的,v的各个分量就是各普通元素的丰度:第1个分量对应着1氢的丰度,第2个分量对应着2氦的丰度,等等。
富度向量w因此也被唯一确定,我们可以定义第n号普通元素的富度是w的第n个分量。从线性代数的观点来看,w和v是相对于同一个特征值的左右特征向量,是对偶的数学对象,所以我们可以把丰度和富度看作是对偶的概念。丰度的英文为abundance,于是和它对偶的富度可以反译回去称作coabundance。
我们不仅可以对普通元素定义其富度,而且可以对一般的普通化合物定义它的富度:普通化合物的富度就是组成它的普通元素的富度之和(同一种元素多次出现则对其富度多次求和)。比如化合物63铕20钙89锕1氢20钙30锌的富度就等于63铕、89锕、1氢、30锌的富度加上两倍20钙的富度。上述定义可以用线性代数的语言简单地写为:令C是一种普通化合物,设它所对应的列向量是u,那么它的富度就是富度向量w和u的内积wu。
在讨论富度的实际意义前,我们先列出所有普通元素的长度、丰度和富度:
| 元素 | 长度 | 丰度 | 富度 |
|---|---|---|---|
| 1氢 | 2 | 0.0917903832 | 5.6080827086 |
| 2氦 | 32 | 0.0032372969 | 3.2519030758 |
| 3锂 | 27 | 0.0042200666 | 2.4945994020 |
| 4铍 | 42 | 0.0022638860 | 4.4173991800 |
| 5硼 | 34 | 0.0029511504 | 3.3886745994 |
| 6碳 | 28 | 0.0038470525 | 2.5995195528 |
| 7氮 | 24 | 0.0050149302 | 1.9941430512 |
| 8氧 | 18 | 0.0065373491 | 1.5297467197 |
| 9氟 | 14 | 0.0085219397 | 1.1734990753 |
| 10氖 | 12 | 0.0111090068 | 0.9002144354 |
| 11钠 | 9 | 0.0144814488 | 0.6905723633 |
| 12镁 | 10 | 0.0188504412 | 1.0642759581 |
| 13铝 | 10 | 0.0245730067 | 0.8164272141 |
| 14硅 | 7 | 0.0320328130 | 0.6262975226 |
| 15磷 | 12 | 0.0148958867 | 1.5173799538 |
| 16硫 | 10 | 0.0194179392 | 1.1640122836 |
| 17氯 | 6 | 0.0253127842 | 0.8929369292 |
| 18氩 | 4 | 0.0329971701 | 0.6849896438 |
| 19钾 | 4 | 0.0430143609 | 0.5254691533 |
| 20钙 | 2 | 0.0560725431 | 0.4030978184 |
| 21钪 | 16 | 0.0093020974 | 2.2191977577 |
| 22钛 | 14 | 0.0121260028 | 1.7023906526 |
| 23钒 | 8 | 0.0158071816 | 1.3059376632 |
| 24铬 | 5 | 0.0206058826 | 1.0018107052 |
| 25锰 | 12 | 0.0268613602 | 1.2489541407 |
| 26铁 | 8 | 0.0350158585 | 0.9580975139 |
| 27钴 | 5 | 0.0456458773 | 0.7349756218 |
| 28镍 | 8 | 0.0138711242 | 1.0277878559 |
| 29铜 | 6 | 0.0180820822 | 0.7884364666 |
| 30锌 | 3 | 0.0235713913 | 0.6048252645 |
| 31镓 | 17 | 0.0014478906 | 2.3774502059 |
| 32锗 | 23 | 0.0018874372 | 2.8607239388 |
| 33砷 | 26 | 2.7246216076 | 2.7242698891 |
| 34硒 | 20 | 3.5517547944 | 2.0898415106 |
| 35溴 | 16 | 4.6299868152 | 1.6031589076 |
| 36氪 | 14 | 6.0355455682 | 1.2298150218 |
| 37铷 | 10 | 7.8678000089 | 0.9434155159 |
| 38锶 | 7 | 1.0256285249 | 0.7237127697 |
| 39钇 | 7 | 1.3369860315 | 0.7923865601 |
| 40锆 | 23 | 1.7428645997 | 2.2353942193 |
| 41铌 | 28 | 2.2719586752 | 2.9203125825 |
| 42钼 | 20 | 2.9616736852 | 2.2402297523 |
| 43锝 | 15 | 3.8607704943 | 1.7185247131 |
| 44钌 | 21 | 3.2899480576 | 2.3970976690 |
| 45铑 | 24 | 4.2887015042 | 2.8757958978 |
| 46钯 | 18 | 5.5906537945 | 2.2060801198 |
| 47银 | 12 | 7.2878492056 | 1.6923278521 |
| 48镉 | 10 | 9.5002745645 | 1.2982182892 |
| 49铟 | 8 | 0.0012384342 | 0.9958890202 |
| 50锡 | 5 | 0.0016143947 | 0.7639662365 |
| 51锑 | 7 | 0.0021044882 | 1.1205778552 |
| 52碲 | 13 | 0.0027433630 | 1.9384007646 |
| 53碘 | 18 | 0.0035761856 | 2.5239203970 |
| 54氙 | 14 | 0.0046618343 | 1.9361494381 |
| 55铯 | 8 | 0.0060770612 | 1.4852586679 |
| 56钡 | 6 | 0.0079219188 | 1.1393714076 |
| 57镧 | 5 | 0.0103268333 | 0.8740344241 |
| 58铈 | 10 | 0.0134618252 | 1.5435278845 |
| 59镨 | 8 | 0.0175485293 | 1.1840708803 |
| 60钕 | 6 | 0.0228758639 | 0.9083242769 |
| 61钷 | 3 | 0.0298204562 | 0.6967935837 |
| 62钐 | 6 | 0.0154081152 | 1.3077219948 |
| 63铕 | 7 | 0.0200856687 | 1.0031795014 |
| 64钆 | 11 | 0.0216629728 | 1.6425976370 |
| 65铽 | 16 | 0.0282393589 | 2.2970039458 |
| 66镝 | 12 | 0.0368121864 | 1.7620773240 |
| 67钬 | 7 | 0.0479875294 | 1.3517244937 |
| 68铒 | 9 | 0.0010985956 | 1.5714588817 |
| 69铥 | 14 | 0.0012049084 | 2.0785360303 |
| 70镱 | 10 | 0.0015706912 | 1.5944862492 |
| 71镥 | 6 | 0.0020475173 | 1.2231620535 |
| 72铪 | 5 | 0.0026690970 | 0.9383118918 |
| 73钽 | 32 | 2.4207736666 | 3.2519030758 |
| 74钨 | 27 | 3.1556655252 | 2.4945994020 |
| 75铼 | 42 | 1.6928801808 | 4.4173991800 |
| 76锇 | 34 | 2.2068001229 | 3.3886745994 |
| 77铱 | 28 | 2.8767344775 | 2.5995195528 |
| 78铂 | 24 | 3.7500456739 | 1.9941430512 |
| 79金 | 18 | 4.8884742983 | 1.5297467197 |
| 80汞 | 14 | 6.3725039755 | 1.1734990753 |
| 81铊 | 12 | 8.3070513293 | 0.9002144354 |
| 82铅 | 9 | 0.0010828883 | 0.6905723633 |
| 83铋 | 10 | 0.0014116286 | 1.0642759581 |
| 84钋 | 10 | 0.0018401670 | 0.8164272141 |
| 85砹 | 7 | 0.0023987998 | 0.6262975226 |
| 86氡 | 12 | 0.0031270209 | 1.5173799538 |
| 87钫 | 10 | 0.0040763134 | 1.1640122836 |
| 88镭 | 6 | 0.0053137895 | 0.8929369292 |
| 89锕 | 4 | 0.0069269352 | 0.6849896438 |
| 90钍 | 4 | 0.0075819047 | 0.5254691533 |
| 91镤 | 2 | 0.0098835986 | 0.4030978184 |
| 92铀 | 1 | 1.0256285249 | 0.3092243383 |
任取一种普通化合物C,设它所对应的列向量是u,那么n天后C演化成的化合物所对应的列向量就是Mnu。根据加强版算术定理的3),我们知道当n趋于无穷时,(1/λn)Mnu会趋于vwu。所以对Mnu在n充分大时的性质的研究可以转化为对vwu的性质的研究。
因为矩阵的乘法满足结合律,所以vwu=v(wu),而上面我们已经知道,wu是w和u的内积,即化合物C的富度,它是一个实数,令它为d,则vwu=dv。这证明了从任何一种普通化合物出发,Mnu在n充分大时和λndv差不多;也就是说,经过足够长时间后,它里面的各元素的百分比就会趋近于丰度向量的各分量。这就是原版算术定理中“每种元素在这些数字串中的比例越来越趋近一个大于0的常数值”这一部分。
我们定义量长向量是这样的行向量,它的各分量分别为各普通元素长度:(2, 32, 27, 42, ……),记它为r。那么容易看出u所对应的化合物的数字串长度就是ru。所以量长向量有测量化合物长度的功能。r和丰度向量v的内积则是一个常量,记它为L,我们可称其为量长常数。(如果滥用一下术语,我们可以说L是丰度向量v所对应的化合物的数字串长度。当然不可能真有哪种化合物所对应的向量会是v,因为v的分量都不是整数,甚至不是有理数。)根据上面的表格容易计算出L≈7.6739102369。对应于Mnu的化合物的长度为rMnu,它约等于rvwuλn=drvλn=dLλn。换句话说,当n相当大时,dLλn是C在n天后演化结果的长度的很好的估计。
这下我们看出来了,dL就是对本节开始想求的c,即化合物的富度乘以量长常数。对11钠,29铜和62钐来说,其富度乘以量长常数的值分别约为5.2993903280,6.0503906721和10.0353412031。这三个数字和前面计算的经验值完全符合。
严格地写成命题的话就有: (量长推论)令普通化合物C的富度为d,它在第n天后演化结果的长度为hn,那么当n趋向于无穷时,dLλn/hn趋向于1,其中L为量长常数。
从这个结论很容易推出原版算术定理中“从任何一个普通化合物开始,每一步演化得到的数字串的长度和上一步相比,越来越趋近于固定常数λ”这部分。于是原版算术定理完全得证。
十一、更多的推论
一件有趣的事情是,如果我们将上面的r由量长向量换成每个分量都是1的行向量(1, 1, 1, 1, ……),那么ru就是u所对应的化合物中的元素个数(于是这个向量我们可以类似地称为计件向量,即以“件数”来称呼化合物中元素的个数),而rv精确地等于1(可称其为计件常数,滥用一下术语的话,丰度向量v所对应的化合物中恰好有1件元素)。对应于Mnu的化合物中的元素件数为rMnu,它约等于rvwuλn=drvλn=dλn。即在n相当大时,dλn是C在n天后演化结果中元素件数的很好的估计。
严格地写成命题的话就有: (计件推论)令普通化合物C的富度为d,它在第n天后演化结果中的元素件数为sn,那么当n趋向于无穷时,dλn/sn趋向于1。
如果再翻译回原版定理的说法,那就是“从任何一个普通化合物开始,每一步演化得到的元素个数和上一步相比,越来越趋近于固定常数λ。”事实上,这才是原版中的原版。康威的论文中的算术定理就是以化合物中元素个数为对象论证的,而不是象在本文上篇中那样,以化合物长度为对象。
这下我们达到了思路广的境界——量长和计件向量只是两个特定的向量而已,而每给定一个92个分量的行向量,上面的论证都可以被照葫芦画瓢地小小改编一下得到一个相应的推论。当然,这个行向量如果随便给就太没意思了,我在下面提几个有某种实际意义的例子。
令C是一个普通化合物,我们定义它的重量是它的所有数字之和。比如1氢的重量是2+2=4,11钠的重量是1+2+3+2+2+2+1+1+2=16。那么我们可以定义称重向量为各分量是各元素重量的行向量(4, 56, 47, 72, ……),定义称重常数则是称重向量和丰度向量v的内积,约等于12.964860969。我们有 (称重推论)令普通化合物C的富度为d,它在第n天后演化结果的重量为wn,那么当n趋向于无穷时,dLλn/hn趋向于1,其中L为称重常数。
类似地我们可以引入“计1向量”、“计2向量”和“计3向量”,其分量分别是各元素中的“1”、“2”和“3”的个数,同样可定义“计1常数”、“计2常数”和“计3常数”,得到类似上面推论的“计1推论”、“计2推论”和“计3推论”。
十二、附记
如果对照康威原论文和本文内容的话,读者会发现在定理和引理的叙述方面有一些不同,最明显的是本文的化学定理变成是完全关于普通化合物的命题了,原本其中关于包含任意字符的数字串的部分,被移动到宇宙学定理中。这样的改动主要是出于科普文介绍的方便,康威从文章一开始就考虑包含任意字符的数字串,而笔者则需要注意循序渐进,以及将不同难度的问题分开。
参考文献:
[1] John Horton Conway, The weird and wonderful chemistry of audioactive decay, Eureka 46:5-16 (1985); reprinted in Open Problems in Communication and Computation, T.M. Cover & B. Gopinath, eds., Springer-Verlag, New York, 173–188 (1987).
[2] Dimitrios Noutsos, On Perron-Frobenius property of matrices having some negative entries, Linear Algebra and its Applications 412:132–153 (2006).