金锞子难题（下）

三、转化为图论问题

首先我们要指出一点，金锞子难题其实就是问，如何制作尽量少的金锞子，使得我们可以在有n人和k人两种情况时，都能平均分配金子。后一种k个人的情况时，其中的n人是否就是前一种情况的那n人（如在上篇问题叙述中那样），是无关紧要的。我们完全可以假定，这n人和k人，都是不同的人。我们分别用A1，A2，……，An，和B1，B2，……，Bk来表示他们。

对每一种符合条件的金锞子制造方案，我们可以画出一个与之对应的平面图来：

首先画出n+k个圆圈，分别标上A1，A2，……，An，和B1，B2，……，Bk，代表这n+k个人。对方案中的每一个金锞子，如果它在n人分配方法中是给Ai的，而在k人分配方法中是给Bj的，那么我们就在Ai和Bj两个圆圈之间连接一条线，并在它的旁边标注它的质量。

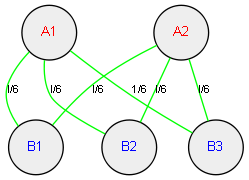
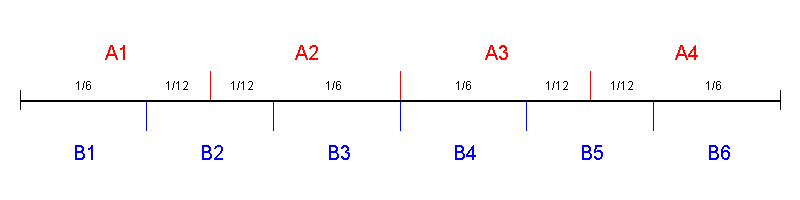
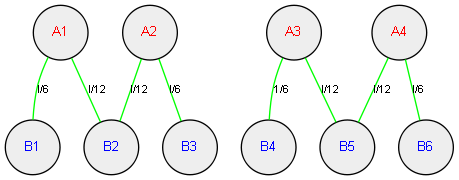
比如在n=2，k=3的情况下，如果制造2*3=6个1/6斤的金锞子，在2人之间分配则每人3个，在3人之间分配则每人2个，那么此方案对应的图如下：

而如果制造4个金锞子，2个1/3斤的，2个1/6斤的。在2人之间分配则每人拿一个1/3的和一个1/6的，在3人之间分配则2个人每人拿一个1/3的，1人拿2个1/6的，那么此方案对应的图如下：

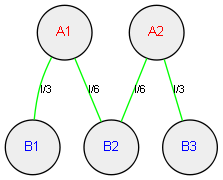
在图论中，这些表示人的圈圈叫顶点，而连接两个人的表示金锞子的线叫边，边上的那些数字叫权，这样的图叫加权图。很明显，在这样一个加权图中，顶点的数目是n+k，而边的数目是金锞子的数目，所有边上的权加起来等于1。

再看一下n=4，k=7的情况。按照第二节的一般方案，我们对长度为1的线段分别进行4等分和7等分，将线段切成如下10段，也即做出10个金锞子：

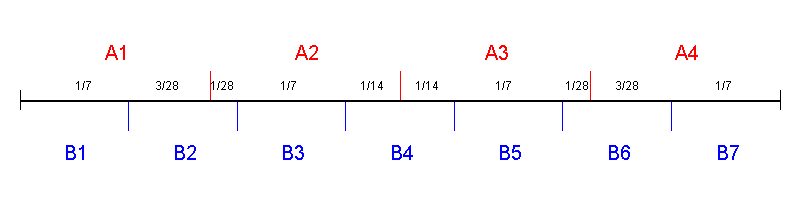
对应的加权图为：

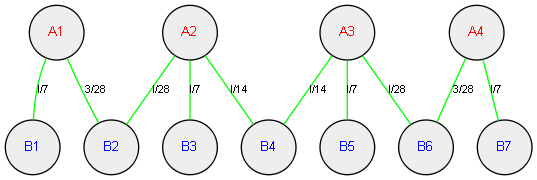
我们注意到，图二和图四都有这样的特点：
1）它们都是连通图，也即从任何一个顶点出发，都可以沿着各边行走，到达其他任意顶点；
2）它们的顶点数恰好比边数多1。
事实上，为了保持“连通图”这个特点，如果顶点数不变，图中的边数已经不可能再少了。任何一个p个顶点的连通图，至少要有p-1条边。这个命题看起来显而易见，是图论中的一个基本结论，在此不证。

一个符合要求的制造金锞子的方案对应的加权图一定是连通的吗？不是。比如在n=4，k=6的情况时，按照第二节的一般方案，我们对长度为1的线段分别进行4等分和6等分，将线段切成如下8段，也即做出8个金锞子：

对应的加权图：

上面这个图分成了不连通的两部分，在图论中，它们被称作是这个图的两个连通分支。

四、证明

很明显，确定了n和k后，如果我们要求一个金锞子数量尽量少的方案，就要使它对应的加权图上的边尽量少，因为边数就是金锞子数。而加权图的顶点数总是n+k，所以要使边尽量少，就要使连通分支尽量多。

如果只有一个连通分支，那么它至少会有n+k-1条边。如果它有两个连通分支，每个分支上的A类顶点数分别为n1和n2（则n1+n2=n），B类顶点数分别为k1和k2（则k1+k2=k），那么它的边至少有(n1+k1-1)+(n2+k2-1)=n+k-2条。事实上，多一个连通分支，加权图至少会有的边就能少一条。

但是符合条件的方案所对应的加权图中的连通分支数并不能随意减少。我们来看看，在这样的加权图中的一个连通分支（也许这个图本身就是连通的，那么它就只有一个连通分支，也就是整个图），必须满足什么样的条件。

假设这个连通分支中分别有n’个A类顶点和k’个B类顶点，所有的边上的权的和为s。那么这实际上是一个可以分别在n’个人和k’个人之间平分s斤金子的方案。每人能得到的金子量，分别都还应是1/n和1/k。这就是说：
    s/n’ = 1/n
    s/k’ = 1/k
于是
    n’k = k’n
令g是n和k的最大公约数，于是我们可以设n=gu，k=gv，其中u和v互素（即最大公约数为1）。代入上式：
    n’gv = k’gu
也即
    n’v = k’u
注意到u和v互素，所以n’必须是u的倍数，k’必须是v的倍数。

如果g=1，那么情况很简单：n=u，k=v。n’小于等于n，又必须是n的倍数，k’小于等于k，又必须是k的倍数。唯一的可能，即n’=n，k’=k，也就是说这个连通分支是唯一的，它就是整个图。此时最优方案是要制造n+k-1个金锞子，所以第二节中的一般方案就是最优方案。比如图二和图四的确是最优方案。

如果g>1，要使连通分支尽量多，而每个分支中A类顶点个数必须是u的倍数，B类顶点个数必须是v的倍数，最好的选择就是g个连通分支，每个分支中A类顶点个数为u，B类顶点个数为v。此时图中的边数至少有g(u+v-1)=n+k-g条，所以第二节中的一般方案仍是最优方案。这个方案其实就是g个相同的能把1/g斤金子平均分配给u个和v个人的小方案。比如图六的最优方案，可以看作是两个相同的图二的方案。